Question

[Pham Trong Bach]

Xét các mệnh đề sau

1   log 2 x − 1 2 + 2 log 2 x + 1 = 6 ⇔ 2 log 2 x − 1 + 2 log 2 x + 1 = 6. 2   log 2 x 2 + 1 ≥ 1 + log 2 x ; ∀ x ∈ ℝ  

3   x ln y = y ln x ;   ∀ x > y > 2.

4   log 2 2 2 x − 4 log 2 x − 4 = 0 ⇔ log 2 2 x − 4 log 2 x − 3 = 0.

Số mệnh đề đúng là

A. 0

B. 1

C. 2

D. 3

Answer 1

[Cao Minh Tâm]

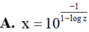
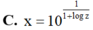
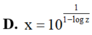
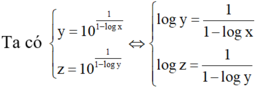
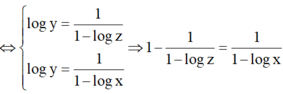
Đáp án C

Dựa vào giả thiết, ta thấy rằng:

  log 2 x − 1 2 + 2 log 2 x + 1 = 6 ⇔ 2 log 2 x − 1 + 2 log 2 x + 1 = 6 ⇒ 1   s a i .

x 2 + 1 ≥ 2 x ⇔ log 2 x 2 + 1 ≥ log 2 2 x = 1 + log 2 x ; ∀ x ∈ ℝ ⇒ 2   đ ú n g  

  x ln y = y ln x ; ∀ x > y > 2 ⇒ 3 đúng.

log 2 2 2 x − 4 log 2 x − 4 = 0 ⇔ log 2 x + 1 2 − 4 log 2 x − 4 = 0 ⇔ log 2 2 − 2 log 2 x − 3 = 0

⇒ 4  sai. Vậy có 2 mệnh đề đúng