Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên SBC là tam giác đều cạnh a và mặt phẳng (SBC) vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng SA và BC là
A. 2 a 2
B. a 2
C. 3 a 4
D. 3 a 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
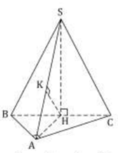

Từ (1), (2) => HK là đoạn vuông góc chung của SA và BC

Tam giác SHA vuông tại A có đường cao HK nên 1 HK 2 = 1 SH 2 + 1 AH 2 = 4 3 a 2 + 4 a 2 = 16 3 a 2 .
⇒ HK = 3 a 4 .

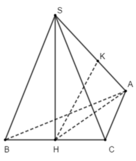
+ Gọi H là trung điểm của BC
Do tam giác ABC cân tại A nên AH ⊥ BC, tam giác SBC đều nên SH ⊥ BC
Mà (SBC) ⊥ (ABC)
Do đó SH ⊥ (ABC)
+ Gọi K là hình chiếu vuông góc của H lên SA ⇒ HK ⊥ SA
Ta có B C ⊥ S H B C ⊥ A H ⇒ B C ⊥ S A H ⇒ B C ⊥ H K
Vậy HK là đoạn vuông góc chung của BC và SA, do đó khoảng cách giữa BC và SA là HK.
+ Tính HK
Tam giác SBC đều cạnh a ⇒ SH = a 3 2
Tam giác ABC vuông cân tại A ⇒ AH = B C 2 = a 2
Tam giác SHA vuông tại H có HK là đường cao ⇒ 1 H K 2 = 1 S H 2 + 1 A H 2
HK = a 3 4
Vậy d(SA; BC) = a 3 4 .
Đáp án C

Nguyễn Khắc Sinh là Nguyen Quang Trung tự hỏi tự trả lời

1) Gọi H là trung điểm của AB.
ΔSAB đều → SH ⊥ AB
mà (SAB) ⊥ (ABCD) → SH⊥ (ABCD)
Vậy H là chân đường cao của khối chóp.

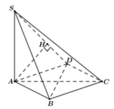
Xác định được ![]()
Khi đó ta tính được ![]()
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật
=> AB//CD nên
Xét tam giác vuông SAD có 
Chọn C.

Chọn C
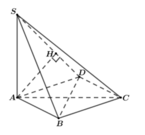
Xác định được
![]()
Khi đó ta tính được
![]()
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật => AB//(SCD) nên
![]()
![]()
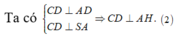
Từ (1) và (2) suy ra
![]()
Xét tam giác vuông SAD có
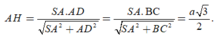
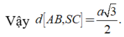
Đáp án C