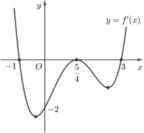
Cho hàm số f(x) có đồ thị f'(x) như hình vẽ bên. Số điểm cực trị của hàm số f(x) là
A. 3.
B. 4.
C. 2.
D. 1.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án B
f'(x) đổi dấu 1 lần, suy ra đồ thị hàm số f(x) có 1 điểm cực trị.

Đáp án C

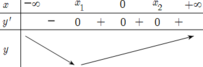
Khi đó hàm số y=f(x) đạt cực tiểu tại x = x 1 hay hàm số y=f(x) có 1 điểm cực trị.

Ta có
![]()
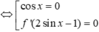
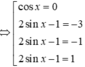
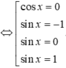
Đối chiếu với
x
∈
-
2
π
;
2
π
nhận 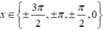 Qua tất cả các điểm này thì y′ đều đổi dấu, do đó hàm số có tất cả 7 điểm cực trị trên khoảng (−2π;2π).
Qua tất cả các điểm này thì y′ đều đổi dấu, do đó hàm số có tất cả 7 điểm cực trị trên khoảng (−2π;2π).
Chọn đáp án C.
Mẹo TN: Chọn ![]() thỏa mãn, khi đó
thỏa mãn, khi đó ![]() MODE 7 trên khoảng (−2π;2π) có 7 lần đổi dấu tức có 7 điểm cực trị trên khoảng (−2π;2π).
MODE 7 trên khoảng (−2π;2π) có 7 lần đổi dấu tức có 7 điểm cực trị trên khoảng (−2π;2π).
Chọn đáp án C.

Chọn đáp án D
![]()
![]()
![]()
![]()
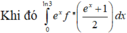

![]()
Do hàm số đạt cực đại tại điểm x=1⇒ f′(1) = 0 và đường thẳng Δ qua hai điểm (0;−3);(1;0) nên có phương trình y=3x−3.
Vì Δ là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 ⇒ f ' ( 2 ) = k △ =3
Vậy