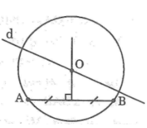
Cho hai điểm A, B và một đường thẳng d. Vẽ đường tròn tâm O đi qua hai điểm A, B sao cho O nằm trên đường thẳng d.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 7 2023
a: góc ACB=1/2*sđ cung AB=90 độ
=>ΔACN vuông cân tại C
góc ACN+góc AMN=180 độ
=>AMNC nội tiếp
b: AMNC nội tiếp
=>góc CNA=góc CMA=góc BMD
góc BNE=1/2(sđ cung BE-sđ cung AC)
góc DMB=1/2*(sđ cung BD-sđ cung AC)
=>sđ cung BD=sđ cung BE
=>B nằm trên trung trực của DE
Xét ΔADB và ΔAEB có
góc ADB=góc aEB
AB chung
DB=BE
=>ΔABD=ΔAEB
=>AD=AE
=>A nằm trên trung trực của DE
=>AB là trung trực của DE
=>DE vuông góc AB
8 tháng 3 2023
1: ΔOAB cân tại O
mà OI là trung tuyến
nên OI vuông góc AB
góc OIM=góc OCM=góc ODM=90 độ
=>O,I,M,D,C cùng thuộc đường tròn đường kính OM
góc DIM=góc MOD
góc CIM=góc COM
mà góc COM=góc DOM
nên góc DIM=góc CIM
=>IM là phân giác của góc CID
28 tháng 5 2023
a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: Xét ΔANB và ΔACN có
góc ANB=góc ACN
góc NAB chung
=>ΔANB đồng dạng với ΔACN
=>AN^2=AB*AC
28 tháng 5 2023
a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: Xét ΔANB và ΔACN có
góc ANB=góc ACN
góc NAB chung
=>ΔANB đồng dạng với ΔACN
=>AN^2=AB*AC
AT
15 tháng 7 2021
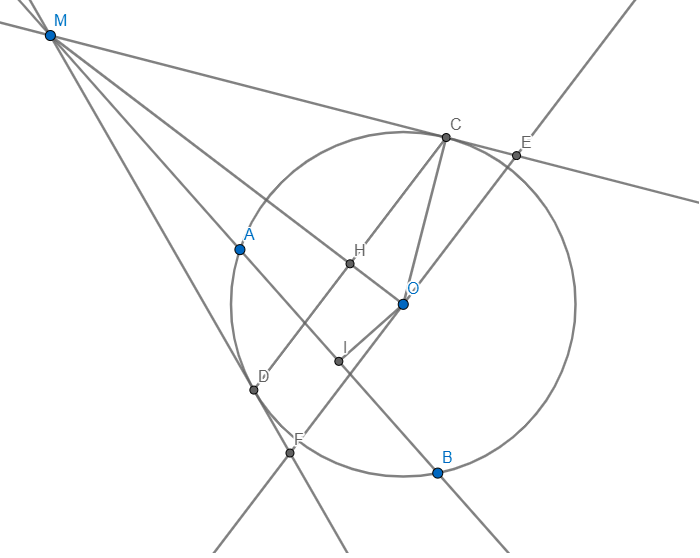
a) Trong (O) có AB là dây cung không đi qua O và I là trung điểm AB
\(\Rightarrow OI\bot AB\Rightarrow\angle MIO=90\Rightarrow\angle MIO+\angle MCO=90+90=180\)
\(\Rightarrow MIOC\) nội tiếp
b) Vì MC,MD là tiếp tuyến \(\Rightarrow\Delta MCD\) cân tại M có MO là phân giác \(\angle CMD\) \(\Rightarrow MO\bot CD\) mà \(EF\parallel CD\) \(\Rightarrow EF\bot MO\)
tam giác MOE vuông tại O có đường cao OC \(\Rightarrow CM.CE=OC^2\)
tam giác MOC vuông tại C có đường cao HC \(\Rightarrow OH.OM=OC^2\)
\(\Rightarrow OH.OM=CM.CE\)
Vì H là trung điểm CD (\(\Delta MCD\) cân tại M) và \(EF\parallel CD\)
\(\Rightarrow O\) là trung điểm EF
\(\Rightarrow S_{MEF}=2S_{MOE}=2.\dfrac{1}{2}.OC.ME=OC.\left(CM+CE\right)\)
\(\ge R.\sqrt{CM.CE}=R.2\sqrt{OC^2}=R.2OC=2R^2\)
\(\Rightarrow S_{MEF_{min}}=2R^2\) khi \(CM=CE=R\left(CM.CE=R^2\right)\)
\(\Rightarrow OM=\sqrt{R^2+R^2}=\sqrt{2}R\)
Vậy M nằm trên d sao cho \(OM=\sqrt{2}R\) thì diện tích tam giác MEF nhỏ nhất \(\left(=2R^2\right)\)
- Vì A và B là hai điểm nằm trên đường tròn tâm O nên OA = OB.
- Suy ra O thuộc đường trung trực của đoạn AB.
Vì tâm O nằm trên đường thẳng d nên O là giao điểm của đường trung trực của AB và đường thẳng d.
- Dựng đường thẳng m là đường trung trực của AB cắt d tại O.
- Vẽ đường tròn tâm O bán kính OA (hoặc OB).
* Lưu ý:
- Nếu m // d thì không dựng được tâm O
- Nếu m trùng với d thì có vô số điểm chung O do đó có vô số đường tròn thỏa mãn bài toán.