Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Phương pháp:
Tính xác suất theo định nghĩa P A = n A n ( Ω ) với n ( A ) là số phần tử của biến cố A, n Ω là số phần tử của không gian mẫu
Cách giải:
Số phần tử của không gian mẫu n Ω = C 9 2
Gọi A là biến cố “rút ra hai thẻ có tích hai số ghi trên hai thẻ là số chẵn”
Khi đó hai thẻ đó hoặc cùng mang số chẵn, hoặc 1 thẻ mang số chẵn và 1 thẻ mang số lẻ.
Trong 9 thẻ đã cho có 4 thẻ mang số chẵn 2;4;6;8 và 5 thẻ mang số lẻ 1;3;5;7;9
Nên số cách rút ra 2 thẻ mang số chẵn là C 4 2
Số cách rút ra 1 thẻ mang số chẵn và 1 thẻ mang số lẻ là
Số phần tử của biến cố A là C 4 1 C 5 1
Chọn C.
Gọi A: “tích 2 số ghi trên 2 thẻ được rút ra là số lẻ” = “cả hai số rút được đều là số lẻ”
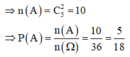
Đáp án A
Rút ngẫu nhiên 2 thẻ trong 9 thẻ có C 9 2 cách ⇒ n ( Ω ) = C 9 2
Gọi X là biến cố “hai thẻ rút được có tích 2 số ghi trên 2 thẻ là số lẻ”
Khi đó 2 thẻ rút ra đều phải đưuọc đánh số lẻ => có C 5 2 cách => n ( X ) = C 5 2 .
Vậy xác suất cần tính là P = n ( X ) n ( Ω ) = C 5 2 C 9 2 = 5 18 .
Đáp án A
Rút ngẫu nhiên 2 thẻ trong 9 thẻ có C 9 2 cách ⇒ n Ω = C 9 2
Gọi X là biến cố “hai thẻ rút được có tích 2 số ghi trên 2 thẻ là số lẻ”
Khi đó 2 thẻ rút ra đều phải đưuọc đánh số lẻ ⇒ có C 5 2 cách ⇒ n X = C 5 2
Vậy xác suất cần tính là P = n X n Ω = C 5 2 C 9 2 = 5 18
Đáp án D
Có 2 trường hợp sau:
+) 1 thẻ ghi số chẵn, 1 thẻ ghi số lẻ, suy ra có C 4 1 . C 5 1 = 20 cách rút.
+) 2 thẻ ghi số chẵn, suy ra có C 4 2 = 6 cách rút.
Suy ra xác suất bằng 20 + 6 C 9 2 = 13 18 .