Cho 2018 số tự nhiên liên tiếp 1, 2, 3, …,2018. Chọn ngẫu nhiên ba số tự nhiên từ các số đã cho. Tính xác suất để chọn được ba số có một số là trung bình cộng của hai số còn lại
A. 3 4034
B. 5 4034
C. 7 4034
D. 9 4034
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Chon 3 số bất kì có C 10 3 = 120 cách
TH1: 3 số chọn ra là 3 số tự nhiên liên tiếp có 8 cách
TH2: 3 số chọn ra là 2 số tự nhiên liên tiếp
+) 3 số chọn ra có cặp (1;2) hoặc (9;10) có 2.7 = 14 cách
+) 3 số chọn ra có cặp ( 2 ; 3 ) ; ( 3 ; 4 ) ; . . . . ( 8 ; 9 ) có 6.6 = 36 cách
Vậy xác suất cần tìm là
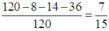

n(S)=6!
Để thỏa mãn yêu cầu đề bài thì cần chọn ra 3 số có tổng là 12
=>Số trường hợp thỏa mãn là (1;5;6); (2;4;6); (3;4;5)
=>Có 3*3!*3!
=>P=3/20

Có A 7 4 = 7 . 6 . 5 . 4 →n(Ω)=7.6.5.4
Số lớn hơn 2018 có 6.6.5.4
Xác suất P=6/7
Đáp án B

Chọn đáp án B
Phương pháp
+) Tính số phần tử của không gian mẫu.
+) Gọi A là biến cố: “Trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp”
=> A “Trong 3 số tự nhiên được chọn có 2 số tự nhiên liên tiếp”.
+) Tính số phần tử của biến cố A .
+) Tính xác suất của biến cố A , từ đó tính xác suất biến cố A.
Cách giải
Chọn ngẫu nhiên 3 số tự nhiên ⇒ n Ω = C 2019 3
Gọi A là biến cố: “Trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp”
=> A : “Trong 3 số tự nhiên được chọn có 2 số tự nhiên liên tiếp”.
Số cách chọn 3 trong 2019 số, trong đó có 2 số tự nhiên liên tiếp, có 2018.2017 cách (có bao gồm các bộ 3 số tự nhiên liên tiếp).
Số cách cả 3 số tự nhiên liên tiếp, có 2017 cách.
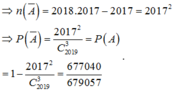

Chọn đáp án D.
Trước hết ta tính số cách chọn 3 số phân biệt từ tập A sao cho không có 2 số nào liên tiếp (gọi số cách đó là M).
+) Ta hình dung có 13 quả cầu xếp thành một hàng dọc (tượng trưng cho 13 số còn lại của A)
+) Giữa 13 quả cầu đó và 2 đầu có tất cả 14 chỗ trống.
Số cách M cần tìm là số cách chọn 3 trong 14 chỗ trống đó, tức bằng C 14 3
Xác suất cần tính là P = C 14 3 C 16 3 = 13 20

Đáp án D
Trước hết ta tính số cách chọn 3 số phân biệt từ tập A sao cho không có 2 số nào liên tiếp (gọi số cách đó là M).
+) Ta hình dung có 13 quả cầu xếp thành 1 hàng dọc (tượng trưng cho 13 số còn lại của A)
+) Giữa 13 quả cầu đó và 2 đầu có tất cả 14 chỗ trống.
Số cách M cần tìm chính là số cách chọn 3 trong 14 chỗ trống đó, tức là bằng C 14 3 .
Xác suất cần tính là P = C 14 3 C 16 3 = 13 20 .