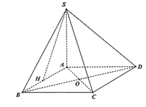
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ABCD). Gọi H là trung điểm của AB, SH = HC, SA = AB. Gọi α là góc giữa đường thẳng SC và mặt phẳng (ABCD). Tính giá trị của tan α .
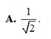

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Hướng dẫn giải: Ta có:
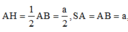
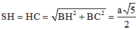
Có A H 2 + S A 2 = 5 a 2 4 = S H 2 ⇒ ∆ S A H vuông tại A
Do đó mà S A ⊥ ( A B C D ) nên
![]()
(Mặt phẳng (SAB) vuông góc với đáy (ABCD))
Trong tam giác vuông SAC, có
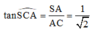

Ta có
A H = 1 2 A B = a 2 ; S A = A B = a S H = H C = B H 2 + B C 2 = a 5 2
Do A H 2 + S A 2 = 5 a 2 4 = S H 2 nên S A ⊥ A B
Do đó S A ⊥ A B C D nên S C , A B C D ^ = S C A ^
Trong tam giác vuông SAC có tan α = tan S C A ^ = S A A C = 1 2
Đáp án A

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=45^0\Rightarrow AC=SA=a\sqrt{2}\)
\(\Rightarrow AB=a\)
Gọi N là trung điểm SA \(\Rightarrow NM||SB\Rightarrow SB||\left(DMN\right)\)
\(\Rightarrow d\left(DM;SB\right)=d\left(SB;\left(DMN\right)\right)=d\left(B;\left(DMN\right)\right)\)
Mà M là trung điểm AB \(\Rightarrow d\left(B;\left(DMN\right)\right)=d\left(A;\left(DMN\right)\right)\)
Từ A kẻ AH vuông góc DM \(\Rightarrow DM\perp\left(NAH\right)\)
Trong mp (NAH), từ A kẻ \(AK\perp NH\Rightarrow AK=d\left(A;\left(DMN\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AM^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{AM.AD}{\sqrt{AM^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AN^2}+\dfrac{1}{AH^2}\Rightarrow AK=\dfrac{AN.AH}{\sqrt{AN^2+AH^2}}=\dfrac{a\sqrt{7}}{7}\)

Đáp án A
Ta có C B ⊥ A B C B ⊥ S A ⇒ C B ⊥ ( S A B )
Do đó S C ; S A B ^ = C S B ^ = α
⇒ S B = a tan α = 5 a 10 ⇒ S A = S B 2 - A B 2 = a 6 2
Ta có S O ; A B C D ^ = S O A ^ trong đó t a n S C A ^ = S A O A = a 6 2 a 2 2 = 3 .

Gợi ý xem bạn làm được ko, ko thì để mình trình bày luôn
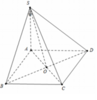
Kẻ \(KC\perp HD;KC\cap HD=\left\{K\right\}\)
\(\left\{{}\begin{matrix}KC\perp HD\\KC\perp SH\end{matrix}\right.\Rightarrow KC\perp\left(SHD\right)\Rightarrow\left(SKC\right)\perp\left(SHD\right)\)
Kẻ \(CI\perp SK;CI\cap SK=\left\{I\right\}\Rightarrow CI\perp\left(SHD\right)\Rightarrow CI\perp\left(SHD\right)\)
\(\Rightarrow\left(SC,\left(SHD\right)\right)=\left(SC,SI\right)\)
Đáp án A