Tổng số điểm biểu diễn nghiệm của phương trình sin 3 x - cos 3 x = sin x - cos x
A.4
B.6
C.5
D.7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

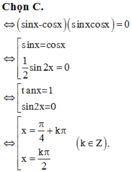

a) Dễ thấy cosx = 0 không thỏa mãn phương trình đã cho nên chiaw phương trình cho cos2x ta được phương trình tương đương 2tan2x + tanx - 3 = 0.
Đặt t = tanx thì phương trình này trở thành
2t2 + t - 3 = 0 ⇔ t ∈ {1 ; ![]() }.
}.
Vậy ![]()
b) Thay 2 = 2(sin2x + cos2x), phương trình đã cho trở thành
3sin2x - 4sinxcosx + 5cos2x = 2sin2x + 2cos2x
⇔ sin2x - 4sinxcosx + 3cos2x = 0
⇔ tan2x - 4tanx + 3 = 0
⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan3 + kπ, k ∈ Z.
+ kπ ; x = arctan3 + kπ, k ∈ Z.
c) Thay sin2x = 2sinxcosx ; ![]() =
= ![]() (sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
(sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
![]() sin2x + 2sinxcosx -
sin2x + 2sinxcosx - ![]() cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔
cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan(-5) + kπ, k ∈ Z.
+ kπ ; x = arctan(-5) + kπ, k ∈ Z.
d) 2cos2x - 3√3sin2x - 4sin2x = -4
⇔ 2cos2x - 3√3sin2x + 4 - 4sin2x = 0
⇔ 6cos2x - 6√3sinxcosx = 0 ⇔ cosx(cosx - √3sinx) = 0
⇔ 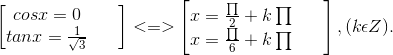

Chọn C
Ta có: ![]() nên (1) và (2) có nghiệm.
nên (1) và (2) có nghiệm.
Cách 1:
Xét: ![]()
![]() nên (3) vô nghiệm.
nên (3) vô nghiệm.
Cách 2:
Điều kiện có nghiệm của phương trình: sin x + cos x = 2 là: 
(vô lý) nên (3) vô nghiệm.
Cách 3:
Vì 

nên (3) vô nghiệm.

Đề lỗi font. Bạn cần chỉnh sửa lại bằng công thức toán để được hỗ trợ tốt hơn.

\(1-2cos^2x-sinx=0\)
\(\Leftrightarrow1-2\left(1-sin^2x\right)-sinx=0\)
\(\Leftrightarrow2sin^2x-sinx-1=0\Rightarrow\left[{}\begin{matrix}sinx=1\\sinx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=-\dfrac{\pi}{6}+k2\pi\\x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{\pi}{2};\dfrac{7\pi}{6};\dfrac{11\pi}{6};\dfrac{5\pi}{2}\right\}\)
\(\Rightarrow\sum x=6\pi\)

\(\dfrac{sin^42x+cos^42x}{tan\left(\dfrac{\pi}{4}-x\right)tan\left(\dfrac{\pi}{4}+x\right)}=cos^4x\)
\(\Leftrightarrow\dfrac{sin^42x+cos^42x}{cot\left(\dfrac{\pi}{4}+x\right)tan\left(\dfrac{\pi}{4}+x\right)}=cos^4x\)
\(\Leftrightarrow sin^42x+cos^42x=cos^4x\)
Giờ hạ bậc nữa là xong rồi. Làm nốt
Hình như đề bạn bị lỗi, thấy chỗ nào cũng ghi là \(cos^44x\).
ĐK: \(x\ne\dfrac{3\pi}{4}+k\pi;x\ne\dfrac{\pi}{4}+k\pi\)
\(\dfrac{sin^42x+cos^42x}{tan\left(\dfrac{\pi}{4}-x\right).tan\left(\dfrac{\pi}{4}+x\right)}=cos^44x\)
\(\Leftrightarrow\dfrac{sin^42x+cos^42x}{\dfrac{sin\left(\dfrac{\pi}{4}-x\right)}{cos\left(\dfrac{\pi}{4}-x\right)}.\dfrac{sin\left(\dfrac{\pi}{4}+x\right)}{cos\left(\dfrac{\pi}{4}+x\right)}}=cos^44x\)
\(\Leftrightarrow\dfrac{sin^42x+cos^42x}{\dfrac{cosx-sinx}{cosx+sinx}.\dfrac{cosx+sinx}{cosx-sinx}}=cos^44x\)
\(\Leftrightarrow sin^42x+cos^42x=cos^44x\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^24x=cos^44x\)
\(\Leftrightarrow cos^44x-\dfrac{1}{2}cos^24x-\dfrac{1}{2}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos^24x=1\\cos^24x=-\dfrac{1}{2}\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{1}{2}cos8x=\dfrac{1}{2}\)
\(\Leftrightarrow cos8x=1\)
\(\Leftrightarrow x=\dfrac{k\pi}{4}\)
Đối chiều điều kiện ban đầu ta được \(x=\dfrac{k\pi}{2}\)