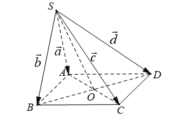
Cho hình hộp đứng A B C D . A ' B ' C ' D ' có đáy là hình bình hành, A B = a , A D = 2 a , B A D ^ = 60 ∘ , A A ' = a 3 . Gọi M , N , P lần lượt là trung điểm của A ' B ' , B D , D D ' và H là hình chiếu của B lên AD. Khoảng cách giữa hai đường thẳng M N , H P bằng
A. a 3 4 .
B. a 3 2 .
C. 2 a 3
D. a 3 .

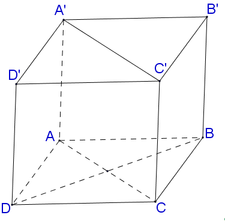
Đáp án A
Qua N vẽ EK song song với A D E ∈ A B , K ∈ D C .
Qua M vẽ MQ song song với A ' D ' Q ∈ D ' C '
Ta có A A ' D ' D / / E M Q K ,mà H P ⊂ A A ' D ' D , M N ⊂ E M Q K nên
d M N , H P = d A A ' D ' D , E M Q K = 1 2 d A ' A D D ' , B ' B C C ' = 1 2 B H = 1 2 a 3 2 = a 3 4 .