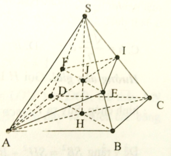
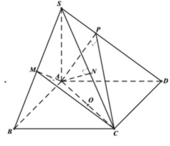
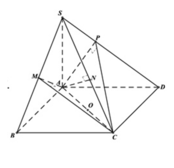
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng a 2 . Mặt phẳng (P) qua A và vuông góc với SC cắt SB, SC, SD lần lượt tại E, I, F. Tính tỉ số k giữa thể tích hình chóp S.AEIF và thể tích hình chóp S.ABCD.
A. k = 1 4
B. k = 1 3
C. k = 1 6
D. k = 2 9


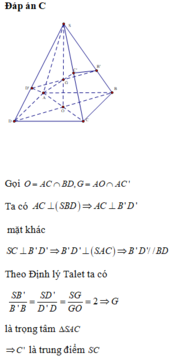
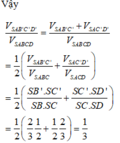
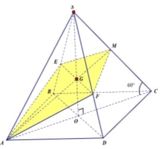
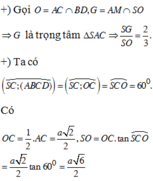

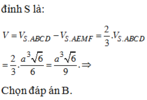




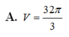
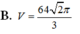
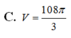



Đáp án B
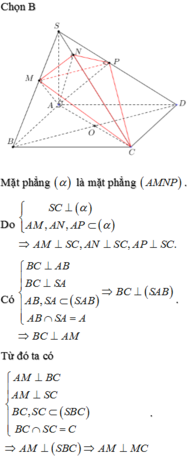
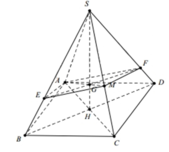
Do các cạnh bên bằng nhau nên hình chiếu của S lên (ABCD) phải trùng với tâm H của hình vuông ABCD.
Dễ thấy I là trung điểm của SC, vì BD ⊥ SC, nên BD//(P). Do đó EF // BD. Để ý rằng EF đi qua trọng tâm J của tam giác SDB.