Cho phân thức A = x 4 + x 3 + x + 1 x 4 − x 3 + 2 x 2 − x + 1 .
a) Thu gọn A.
b) Chứng minh A luôn không âm với mọi giá trị của x.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
20 tháng 3 2019
Đúng(0)
Những câu hỏi liên quan
PT
1
5 tháng 12 2021
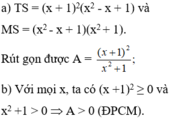
\(a,\dfrac{x^3-2^3}{x^2-4}=\dfrac{\left(x-2\right)\left(x^2-2x+4\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2-2x+4}{x+2}\\ b,\dfrac{2}{2x-4}=\dfrac{2}{2\left(x-2\right)}=\dfrac{1}{x-2}\\ \dfrac{3}{3x-6}=\dfrac{3}{3\left(x-2\right)}=\dfrac{1}{x-2}\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2023
1.
\(A=\dfrac{2x-9}{\left(x-2\right)\left(x-3\right)}-\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-2\right)\left(x-3\right)}+\dfrac{\left(2x+4\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{2x-9-\left(x^2-9\right)+\left(2x^2-8\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x^2+2x-8}{\left(x-2\right)\left(x-3\right)}=\dfrac{\left(x-2\right)\left(x+4\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x+4}{x-3}\)
b.
\(A=2\Rightarrow\dfrac{x+4}{x-3}=2\Rightarrow x+4=2\left(x-3\right)\)
\(\Rightarrow x=10\) (thỏa mãn)
2.
\(x^4+2x^2y+y^2-9=\left(x^2+y\right)^2-3^2=\left(x^2+y-3\right)\left(x^2+y+3\right)\)
26 tháng 12 2021
a: \(A=\dfrac{x+4x+8+x-2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x+2\right)}{3\left(x+1\right)}\)
\(=\dfrac{6\left(x+1\right)\cdot x}{3\left(x+1\right)\left(x-2\right)}=\dfrac{2x}{x-2}\)
10 tháng 9 2018
1/(x+2)(x+3)(x+4)(x+5)-24
=(x+2)(x+5)(x+3)(x+4)
=(x+2)(x-2+7)(x+3)(x-3+7)
=[(x+2)(x-2)+7x+14][(x+3)(x-3)+7x+21]
=(x2-4+7x+14)(x2-9+7x+21)
=(x2+10+7x)(x2+12+7x)
2/(x2+x)2+4(x2+x)-12
=(x2+x)2+4(x2+x)+22-16
=(x2+x+2)2-42
=(x2+x+2+4)(x2+x+2-4)
=(x2+x+6)(x2+x-2)
3/(x2+x+1)(x2+x+2)-12
=(x2+x+1)(x2+x+-1+3)-12
=(x2+x+1)(x2+x+-1)+3(x2+x+1)-12
=(x2+x)-1+3(x2+x)+3-12
=(x2+x)(x2+x+3)-10
làm đến đây thì mk bí, bạn giúp suy nghĩ nốt nha
4/nó là nhân tử sẵn rồi mà
9 tháng 8 2021
\(3/\)
\(\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
\(=\left(x^2+x+1\right)\left(x^2+x+1+1\right)-12\)
\(=\left(x^2+x+1\right)^2+x^2+x+1-12\)
\(=\left(x^2+x+1\right)^2+4\left(x^2+x+1\right)-3\left(x^2+x+1\right)-12\)
\(=\left(x^2+x+1\right)\left(x^2+x+1+4\right)-3\left(x^2+x+1+4\right)\)
\(=\left(x^2+x+1-3\right)\left(x^2+x+1+4\right)\)
\(=\left(x^2+x-2\right)\left(x^2+x+5\right)\)
