Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A và D, AD= DC = a . SAB là tam giác đều cạnh 2a và mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD). Tính cosin của góc giữa hai mặt phẳng (SAB) và (SBC)
A. 2 7
B. 2 6
C. 3 7
D. 5 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là A
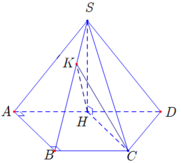
Gọi H là trung điểm của A B . Gọi K là hình chiếu vuông góc của H lên S B .
Khi đó, C K H ^ là góc giữa hai mp
Ta có: S H = 2 a 3 2 = a 3 ; S B = 2 a ; H B = a ⇒ H K = a 3 2 ; C K = a 7 2 .
Vậy cos C K H ^ = 3 7

Chọn đáp án C
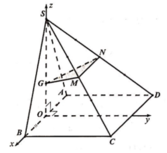
Gọi O là trung điểm AB.
Do tam giác SAB đều và nằm trong mặt phẳng vuông góc (ABCD) nên![]()
Chọn hệ trục tọa độ Oxyz như hình vẽ. Chọn a = 2.
Khi đó: ![]()
![]()
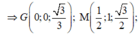
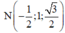
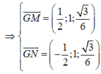
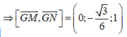
Ta có mặt phẳng (ABCD) có vecto pháp tuyến là ![]()
Mặt phẳng (GMN) có vecto pháp tuyến là 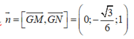
Gọi α là góc giữa hai mặt phẳng (GMN) và (ABCD)
Ta có:
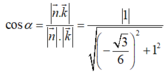
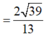

Chọn đáp án C
Gọi O là trung điểm AB.
Do tam giác SAB đều và nằm trong mặt phẳng vuông góc (ABCD) nên S O ⊥ A B C D
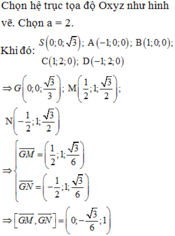
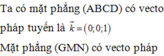

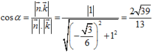

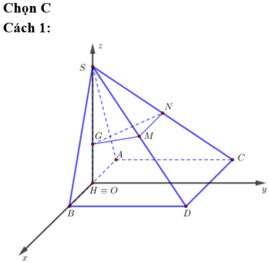
Chọn hệ trục tọa độ Oxyz như hình vẽ. Khi đó
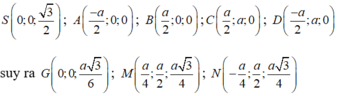
Ta có mặt phẳng (ABCD) có vectơ pháp tuyến là ![]() , mặt phẳng (GMN) có vectơ pháp tuyến là
, mặt phẳng (GMN) có vectơ pháp tuyến là 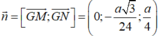
Gọi (α) là góc giữa hai mặt phẳng (GMN) và (ABCD), ta có
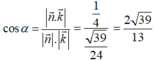
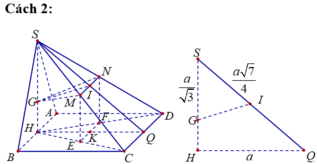
Gọi E, F lần lượt là hình chiếu của M và N lên (ABCD). Suy ra E, F lần lượt là trung điểm của HC, HD.
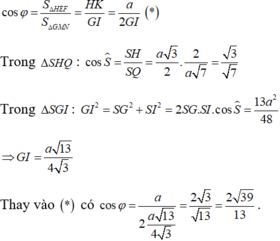
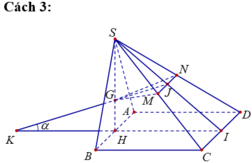
Gọi H, I lần lượt là trung điểm của AB, CD.
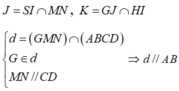
Mà d ⊥ (SIH) nên góc giữa góc giữa hai mặt phẳng (GMN) và (ABCD) là ![]()
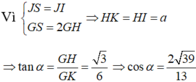

Đáp án B

Vì ABCD là hình vuông ⇒ A B ⊥ A D 1
Ta có S A B ⊥ A B C D S A C ⊥ A B C D ⇒ S A ⊥ A B C D ⇒ S A ⊥ A B 2
Từ (1), (2) suy ra A B ⊥ S A D ⇒ S B ; S A D ^ = S B ; S A ^ = B S A ^
Tam giác SAB vuông tại A, có cos B S A ^ = S A S B = S A S A 2 + A B 2 = 2 5 5 .

Chọn B.
Phương pháp: Sử dụng định nghĩa góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
