Số véctơ khác 0 → có điểm đầu và điểm cuối là hai trong 6 đỉnh của lục giác ABCDEF là
A. P 6
B. 36
C. C 6 2
D. A 6 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
7 tháng 8 2021
Câu 5:
D. Các vector \(\overrightarrow{AB}, \overrightarrow{BA}, \overrightarrow{AC}, \overrightarrow{CA}, \overrightarrow{BC}, \overrightarrow{CB}\)
5 tháng 4 2017
Giải:
Vì lấy 2 điểm nên:
\(C^2_6=15\rightarrow n\left(\Omega\right)=15\)
Gọi:
\(A\) là biến cố "2 thẻ lấy ra là 2 cạnh của lục giác"
\(B\) là biến cố "2 thẻ lấy ra là đường chéo của lục giác"
\(C\) là biến cố "2 thẻ lấy ra là đường chéo của 2 cạnh đối diện của lục giác"
a) \(n\left(A\right)=6\Rightarrow P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{6}{15}=\dfrac{2}{5}\)
b) \(B=\overline{A}\Rightarrow P\left(B\right)=1-P\left(A\right)=1-\dfrac{2}{5}=\dfrac{3}{5}\)
c) \(n\left(C\right)=6\Rightarrow P\left(C\right)=\dfrac{n\left(C\right)}{n\left(\Omega\right)}=\dfrac{3}{15}=\dfrac{1}{5}\)
AH
Akai Haruma
Giáo viên
19 tháng 10 2018
Lời giải:
Các vecto khác vecto $0$ mà cùng phương với \(\overrightarrow{OC}\) có điểm đầu điểm cuối là đỉnh lúc giác là:
\(\overrightarrow{AB};\overrightarrow{BA};\overrightarrow{FC};\overrightarrow{CF}; \overrightarrow{ED};\overrightarrow{DE}\)
Đáp án B
BT
18 tháng 5 2017
Số các véc tơ khác \(\overrightarrow{0}\) bằng véc tơ \(\overrightarrow{OC}\) có điểm đầu và điểm cuối là đỉnh lục giác là:
\(\overrightarrow{AB};\overrightarrow{BA};\overrightarrow{FO};\overrightarrow{OF};\overrightarrow{ED};\overrightarrow{DE};\overrightarrow{FC};\overrightarrow{CF}\).
Có 8 véc tơ.
CM
22 tháng 12 2018
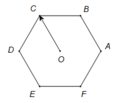
Các vecto cùng phương O C → với có điểm đầu và điểm cuối là các đỉnh của lục giác
: .
Chọn C.
Đáp án D
Với hai đỉnh bất kì trong 6 đỉnh đã cho tạo được 2 vecto. Số vecto cần tính là A 6 2