Hai đường thẳng AB và CD cắt nhau tại M tạo thành A M C ^ có số đo bằng 30°.
a) Tính số đo các góc B M D ^ và A M D ^ .
b) Viết tên các cặp góc đối đỉnh và các cặp góc bù nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
15 tháng 10 2018
Đúng(0)
Những câu hỏi liên quan
HT
18 tháng 7 2019
Bạn tự vẽ hình nhé !!!
- TA có : \(\widehat{AMC}=\widehat{BMD}=30\)độ ( Đối đỉnh )
Vì góc AMD và góc BMD kề bù nên :
<=> Góc AMD + góc BMD = 180 độ
<=> góc AMD = 150 độ
b) Cặp đóc đối đỉnh : góc AMC và BMD
góc AMD và BMC
Cặp góc bù nhau : góc ACM và AMD
góc BMD và BMC
= 60°.
có số đo bằng 30°.
và 
.
= 40°.
, 
và 
9 tháng 10 2016
a) Vì AOC + BOC = 180 độ
và BOC + BOD = 180 độ
=> AOC = BOD ( 2 góc đối đỉnh )
mà AOC = 45*
=> BOD = 45*
Vì AOD và AOC là 2 góc kề bù ( CD cắt AB tại O )
=> AOD + AOC = 180*
Thay AOC = 45*
=> AOD = 180* - 45* = 135*
b) Các cặp góc bù nhau là:
+ AOC và BOC.
+ BOC và BOD
+ BOD và AOD
+ AOD và AOC
18 tháng 4 2018
a. Ta có:
∠NAQ và ∠PAM là hai góc đối đỉnh
Suy ra:∠NAQ = CPAM
mà ∠PAM = 33o nên ∠NAQ = 33o
b. ∠PAM và ∠MAQ là hai góc kề bù nên ∠PAM + ∠MAQ=180o
Suy ra: ∠MAQ = 180o-∠PAM =180o-33o=147o
c. Các cặp góc đối đỉnh là: ∠PAM và ∠NAQ ; ∠PAN và ∠MAQ
d. Các cặp góc kề bù là: ∠PAM và ∠MAQ; ∠PAM và ∠PAN ; ∠NAQ và ∠PAN ; ∠NAQ và ∠QAM
18 tháng 4 2018
a. Ta có:
∠NAQ và ∠PAM là hai góc đối đỉnh
Suy ra:∠NAQ = CPAM
mà ∠PAM = 33o nên ∠NAQ = 33o
b. ∠PAM và ∠MAQ là hai góc kề bù nên ∠PAM + ∠MAQ=180o
Suy ra: ∠MAQ = 180o-∠PAM =180o-33o=147o
c. Các cặp góc đối đỉnh là: ∠PAM và ∠NAQ ; ∠PAN và ∠MAQ
d. Các cặp góc kề bù là: ∠PAM và ∠MAQ; ∠PAM và ∠PAN ; ∠NAQ và ∠PAN ; ∠NAQ và ∠QAM
6 tháng 7 2019
a) Ta thấy : AOD + COA = 180 độ ( kề bù)
Giả sử AOD < COA
=> 2AOD < AOD + COA = 180 độ
=> AOD < 180 : 2 = 90 độ
Mà AOD = COB ( đối đỉnh)
=> Trong các góc trên có 2 góc có số đo là 90 độ
b) Trong 3 góc bất kì luôn luôn có 2 kề bù
=> Tổng 2 góc nó = 180 độ
=> Góc còn lại là : 225- 180 = 45 độ
Góc kề bù với nó là : 180 - 45 = 135 độ
NH
6 tháng 7 2019
a, Giả sử không tồn tại góc nào có số đo ≤ 90o
=> Cả 4 góc có số đo > 90o
=> Tổng số đo của 4 góc > 360o ( Vô lý )
Vậy tồn tại ít nhất 1 góc có số đo ≤ 90o mà góc này có góc đối đỉnh với nó
=> tồn tại 2 góc ≤ 90o ( đpcm )
b, Gỉa sử \(\widehat{O_1}+\widehat{O_2}+\widehat{O_3}=225^o\)
Mà \(\widehat{O_1}+\widehat{O_2}=180^o\)( 2 góc kề bù )
\(\Rightarrow\widehat{O_3}=225^o-180^o=45^o\)
Mà \(\widehat{O_1}=\widehat{O_3}\)( 2 góc đối đỉnh )
\(\Rightarrow\widehat{O_1}=45^o\)
Lại có: \(\widehat{O_1}+\widehat{O_2}=180^o\)
\(\Rightarrow45^o+\widehat{O_2}=180^o\)
\(\Rightarrow\widehat{O_2}=135^o\)
Mà \(\widehat{O_4}=\widehat{O_2}\)( 2 góc đối đình )
\(\Rightarrow\widehat{O_4}=135^o\)
CM
11 tháng 2 2018
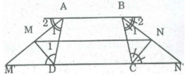
MN = (AB + M’N') / 2 (tính chất đường trung hình hình thang)
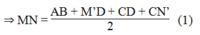
Mà M'D = AD, CN' = BC.
Thay vào (1) : 
