Trong không gian với hệ tọa độ Oxyz cho A (1; 2; -3), B (3/2; 3/2; -1/2), C (1; 1; 4), D (5; 3; 0). Gọi (S1) là mặt cầu tâm A bán kính bằng 3, (S2) là mặt cầu tâm B bán kính bằng 3/2. Có bao nhiêu mặt phẳng tiếp xúc với 2 mặt cầu (S1), (S2) đồng thời song song với đường thẳng đi qua 2 điểm C, D.
A. 1
B. 2
C. 4
D. Vô số.

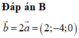

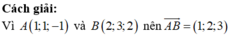

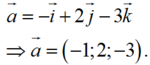
Chọn A
Cách 1:
Cách 2: Ta có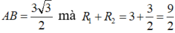 nên hai mặt cầu cắt nhau theo một đường tròn giao tuyến.
nên hai mặt cầu cắt nhau theo một đường tròn giao tuyến.
Gọi I = AB ∩ (α) với (α) là mặt phẳng thỏa mãn bài toán.
Hạ vuông góc với mặt phẳng .
Khi đó ta có I nằm ngoài AB và B là trung điểm AI vì
Suy ra I (2;1;2). Gọi (α): a(x-2) + b(y-1) + c(z-2) = 0.
Vì (α) // CD mà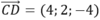 nên ta có 2a + b - 2c = 0 => b = 2c - 2a
nên ta có 2a + b - 2c = 0 => b = 2c - 2a
Ta có hai trường hợp:
Nếu b = -2c; a = 2c => (α): 2c (x-2) + 2c (y-1) + c(z-2) = 0 => 2x - 2y + z - 4 = 0
Mặt khác CD // (α) nên CD ∉ (α) loại trường hợp trên.
Nếu b = c; a = c/2 => (α): c/2 . (x-2) + c (y-1) + c(z-2) = 0 => x + 2y + 2z - 8 = 0
Kiểm tra thấy CD ∉ (α) nên nhận trường hợp này. Vậy (α): x + 2y + 2z - 8 = 0