Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SC. Biết thể tích của khối chóp S.BMN là a 3 . Tính thể tích khối chóp S.ABCD A. a...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

PT

Pham Trong Bach

10 tháng 2 2019

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SC. Biết thể tích của khối chóp S.BMN là a 3 . Tính thể tích khối chóp S.ABCD A. a 3 B. 4 a 3 C. 8 a 3 D. 16 a 3 ...

#Toán lớp 12

1

CM

Cao Minh Tâm

10 tháng 2 2019

Đáp án C

Theo tỉ số thể tích ta có:

Những câu hỏi liên quan

HP

hoàngbaby pham

27 tháng 6 2021

cho hình chóp s.abcd có ABCD là hình bình hành. M,N,P,Q lần lượt là trung điểm của SA,SB,SC,SD. Tí số thể tích của khối chóp S.MNPQ và khối chóp S.ABCD

#Toán lớp 12

1

NV

Nguyễn Việt Lâm

Giáo viên

27 tháng 6 2021

Theo công thức Simsons ta có:

\(\dfrac{V_{SMNPQ}}{V_{SABCD}}=\dfrac{2V_{SMNP}}{2V_{SABC}}=\dfrac{SM}{SA}.\dfrac{SN}{SB}.\dfrac{SP}{SC}=\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{8}\)

TA

Thao An

27 tháng 6 2021

công thức Simsons chỉ áp dụng với khối chóp tam giác thôi mà ạ?

TT

Thư Trần

25 tháng 6 2023

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của AC và BD. Gọi M, N lần lượt là trung điểm của SB, SC. Tính tỉ số thể tích giữa hai khối chóp O.BCNM và...

#Toán lớp 11

1

H

HaNa

25 tháng 6 2023

Tự vẽ hình nhé!

Ta có:

\(V_{OBCNM}=\dfrac{1}{3}d\left(O;\left(BCNM\right)\right).S_{BCNM}=\dfrac{1}{3}.\dfrac{1}{2}d\left(A;\left(SBC\right)\right).\dfrac{3}{4}S_{SBC}=\dfrac{1}{8}V_{SABC}=\dfrac{1}{16}V_{SABCD}\)

\(\Rightarrow\dfrac{V_{OBCNM}}{V_{SABCD}}=\dfrac{1}{16}\)

PT

Pham Trong Bach

1 tháng 9 2017

Cho hình chóp S.ABCD, gọi M, N, P, Q lần lượt là trung điểm của các cạnh SA, SB, SC, SD. Tính thể tích khối chóp S.ABCD biết thể tích khối chóp S.MNPQ là 1.

A.16

B. 8

C. 2

D. 4

1

CM

Cao Minh Tâm

1 tháng 9 2017

Chọn B.

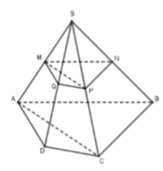
Phương pháp

Sử dụng công thức tính tỉ số thể tích đối với khối chóp tam giác

Chú ý: Công thức tỉ số thể tích trên chỉ áp dụng đối với chóp tam giác.

PT

Pham Trong Bach

16 tháng 12 2019

Cho hình chóp S.ABCD, gọi M, N, P, Q lần lượt là trung điểm của các cạnh SA, SB, SC, SD. Tính thể tích khối chóp S.ABCD biết thể tích khối chóp S.MNPQ là 1. ...

#Toán lớp 12

1

CM

Cao Minh Tâm

16 tháng 12 2019

PT

Pham Trong Bach

15 tháng 2 2017

Cho hình chóp S.ABCD có S A = a , S B = 2 a , S C = 3 a và A S B ⏜ = A S C ⏜ = B S C ⏜ = 60 o . Biết đáy ABCD là hình bình hành. Tính thể tích V của khối chóp S.ABCD. A. V = a 3 2 B. V ...

1

CM

Cao Minh Tâm

15 tháng 2 2017

Chọn đáp án A

Áp dụng công thức

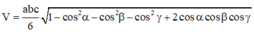
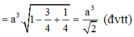
Suy ra V S . A B C D = a 2 2 ( đ v t t )

PT

Pham Trong Bach

18 tháng 2 2017

Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Biết SA vuông góc với mặt đáy, SB = 2a. Gọi M, N lần lượt là trung điểm SB, BC. Tính thể tích V của khối chóp A.SCNM? A. V = a 3 3 16 B. C C. V = a 3 3 24 D. V = a 3 3 8 ...

#Toán lớp 12

1

CM

Cao Minh Tâm

18 tháng 2 2017

Đáp án D

Hướng dẫn giải:

Ta có S A B C = a 2 2 , S A = S B 2 - A B 2 = a 3

V S . A B C = 1 3 S A . S A B C = 1 3 a 3 . a 2 2 = a 3 3 6

Ta lại có V B . N A M V B . C A S = B N B C . B M B S = 1 4

⇒ V B . N A M = 1 4 V B . C A S

Kết luận V A . S C N M = V S . A B C - V B . N A M = a 3 3 8

PT

Pham Trong Bach

1 tháng 3 2019

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm của AD. Gọi S ' là giao điểm của SC với mặt phẳng chứa BM và song song với SA. Tính tỉ số thể tích của hai khối chóp S'.BCDM và S.ABCD. A. 2 3 B. 1 2 C. 1 4 D. 3 4 ...

#Toán lớp 12

1

CM

Cao Minh Tâm

1 tháng 3 2019

Chọn B

PT

Pham Trong Bach

5 tháng 1 2020

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm của AD. Gọi S' là giao điểm của SC với mặt phẳng chứa BM và song song với SA. Tính tỉ số thể tích của hai khối chóp S'.BCDM và S.ABCD A. 2 3 B. 1 2 C. 1 4 D. 3 4 ...

1

CM

Cao Minh Tâm

5 tháng 1 2020

PT

Pham Trong Bach

14 tháng 4 2019

Cho khối chóp S.ABCD có đáy ABCD là hình vuông. Gọi M, N, P, Q lần lượt là trung điểm của SB, BC, CD, DA. Biết thể tích khối chóp S.ABCD là V o . Tính thể tích V của khối chóp M.QPCN theo V o ...

#Toán lớp 11

1

CM

Cao Minh Tâm

14 tháng 4 2019

Đáp án C