Lập phương trình của đường thẳng ∆ đi qua giao điểm của hai đường thẳng d1: x + 3y – 1 =0 d2: x – 3y - 5= 0 và vuông góc với đường thẳng d3: 2x - y + 7 = 0.
A. 3x + 6y - 5=0.
B. 6x + 12y - 5 = 0.
C. 6x+ 12y + 10 = 0.
D. x +2y + 10 = 0.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
19 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
LA
31 tháng 3 2020
a) Giao điểm d1 và d2
\(\left\{{}\begin{matrix}x+3y-1=0\\x-3y-5=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=1\end{matrix}\right.\) => A (-2;1)
Đường thẳng d3 có \(\overrightarrow{n_{d3}}=\left(2;-1\right)\) . Delta vuông góc với d3 nên có
\(\overrightarrow{u_{\Delta}}=\left(2;-1\right)\) \(\Rightarrow\overrightarrow{n_{\Delta}}=\left(-1;-2\right)\)
PTđt delta
\(-1\left(x+2\right)+\left(-2\right)\left(y-1\right)=0\)
\(\Leftrightarrow-x-2y+1=0\)
b) Tương tự, tìm được đường thẳng delta đi qua B(-1;-1)
Hệ số k = tan45 = 1 .
Tự xử nốt
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
Giao điểm A của d1 và d2 là nghiệm:
\(\left\{{}\begin{matrix}x+2y+1=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=11\\y=-6\end{matrix}\right.\)
\(\Delta\) song song d3 nên nhận (2;3) là 1 vtpt, nên có pt:
\(2\left(x-11\right)+3\left(y+6\right)=0\Leftrightarrow2x+3y-4=0\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 4 2019
Giao điểm A của d1 và d2 là nghiệm của hệ:
\(\left\{{}\begin{matrix}x-2y+5=0\\2x-3y+7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\) \(\Rightarrow A\left(1;3\right)\)
Do \(d//d_3\Rightarrow d\) nhận \(\overrightarrow{n_d}=\left(3;4\right)\) là 1 vtpt
Phương trình d:
\(3\left(x-1\right)+4\left(y-3\right)=0\Leftrightarrow3x+4y-15=0\)
CM
11 tháng 3 2017
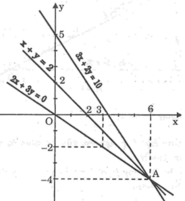
Vẽ đường thẳng ( d 1 ) là đồ thị hàm số y = -x + 2
Cho x = 0 thì y = 2 ⇒ (0; 2)
Cho y = 0 thì x = 2 ⇒ (2; 0)
Vẽ đường thẳng (
d
2
) là đồ thị hàm số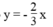 
Cho x = 0 thì y = 0 ⇒ (0; 0)
Cho x = 3 thì y = -2 ⇒ (3; -2)
Hai đường thẳng ( d 1 ) và ( d 2 ) cắt nhau tại A(6; -4). Thay các giá trị x và y này vào phương trình đường thẳng ( d 3 ), ta có:
3.6 + 2.(-4) = 18 – 8 = 10.
Vậy x và y thỏa phương trình 3x + 2y = 10 nên (x; y) = (6; -4) là nghiệm của phương trình 3x + 2y = 10.
13 tháng 2 2016
d1 có 1 vtpt là \(\overrightarrow{n1}\)(2;-1);d2 có 1 vtpt là \(\overrightarrow{n2}\)(3;6)
Ta có \(\overrightarrow{n1}\)\(\times\)\(\overrightarrow{n2}\)=2\(\times\)3-1\(\times\)6=0 nên d1 vuông góc d2 và d1 cắt d2 tại I(I khác P)
Gọi d là đườg thẳng đi qua P;d:A(x-2)+B(y+1)=0\(\Leftrightarrow\)Ax+By-2A+B=0
d cắt d1;d2 tạo thành một tam giác cân có đỉnh I\(\Leftrightarrow\)d tạo với d1(hoặc d2) một góc 45
\(\Leftrightarrow\)\(\frac{\left|2A-B\right|}{\sqrt{A^2+B^2}\sqrt{2^2+\left(-1\right)^2}}\)=\(\cos45\)
\(\Leftrightarrow\)\(3A^2\)-8AB-\(3B^2\)=0
\(\Leftrightarrow\)A=3B hoặc B=-3A
Nếu A=3B ta có d:3x+y-5=0
Nếu B=-3A to có d:x-3y-5=0
Vậy......
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 2 2021
Gọi \(M\left(x;y\right)\) là điểm cách đều \(d_1\) và \(d_2\)
\(\Rightarrow\dfrac{\left|2x-y+5\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{\left|3x+6y-1\right|}{\sqrt{3^2+6^2}}\)
\(\Leftrightarrow\left|6x-3y+15\right|=\left|3x+6y-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-9y+16=0\\9x+3y+14=0\end{matrix}\right.\)
\(\Rightarrow\) Phương trình đường thẳng cần tìm có dạng:
\(\left[{}\begin{matrix}9\left(x+2\right)+3\left(y-0\right)=0\\3\left(x+2\right)-9\left(y-0\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+y+6=0\\x-3y+2=0\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 4 2019
Gọi M là giao điểm của \(d_1\) và \(d_2\Rightarrow\) toạ độ M là nghiệm của hệ:
\(\left\{{}\begin{matrix}3x-2y+5=0\\2x+4y-7=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{3}{8};\frac{31}{16}\right)\)
Do \(d//d_3\Rightarrow d\) nhận \(\overrightarrow{n_d}=\left(3;4\right)\) là 1 vtpt
Phương trình d:
\(3\left(x+\frac{3}{8}\right)+4\left(y-\frac{31}{16}\right)=0\Leftrightarrow24x+32y-53=0\)
