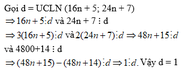c) Chứng tỏ rằng: 16 n + 5 24 n + 7 là phân số tối giản với mọi n ∈ N
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
29 tháng 8 2018
Đúng(0)
Những câu hỏi liên quan
NT
3
26 tháng 6 2015
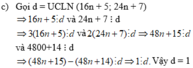
Đặt ƯCLN\(\left(16n+5;24n+7\right)=d\)
=> 16n + 5 chia hết cho d và 24n + 7 chia hết cho d.
=> 3.(16n + 5) - 2.(24n + 7) chia hết cho d.
=> 48n + 15 - 38n + 14 chia hết cho d
=> 1 chia hết cho d
=> d = 1
suy ra điều phải chứng tỏ
VD
29 tháng 3 2017
Gọi d là UCLN(16n+5;24n+7)
=>16n+5 chia hết cho d và 24n+7 chia hết cho d
Vì:16n+5 chia hết cho d=>48n+15 chia hết cho d
24n+7 chia hết cho d=>48n+14 chia hết cho d
Ta có:(48n+15)-(48n+14) chia hết cho d
= 1 chia hết cho d
Vì d=1 nên \(\frac{18n+5}{24n+7}\)là phân số tối giản với mọi n.
Mình làm bài này rồi,đề thi HSG lớp 6 có bài này.
PT
1
MY
2
1 tháng 5 2021
Giả sử UCLN(14n+3;21n+5)=d
14n+3 chia hết cho d nên 42n+9 chia hết cho d
21n+5 chia hết cho d nên 42n+10 chia hết cho d
vay 1 chia hết cho d, d=1
Vậy phân số tối giản
1 tháng 5 2021
Giải:
Gọi ƯC(14n+3;21n+5)=d
⇒14n+3 ⋮ d ⇒3.(14n+3) ⋮ d ⇒42n+9 ⋮ d
21n+5 ⋮ d 2.(21n+5) ⋮ d 42n+10 ⋮ d
⇒(42n+10)-(42n+9) ⋮ d
⇒ 1 ⋮ d
⇒d=1
Vậy 14n+3/21n+5 là phân số tối giản.
Chúc bạn học tốt!
HT
1
LT
0
NP
1
N
6 tháng 1 2022
Giải:
Gọi ƯCLN (2n+3;3n+5)=d
Ta có:
2n+3:d =>3. (2n+3):d
3n+5:d=> 2. (3n+5):d
=> [3. (2n+3) - 2.(3n+5)]:d
=>(6n+9 - 6n-10): d
=> -1:d
=> d={1,-1}
Tick mình nha
TO
2
1 tháng 4 2017
goi d la UCLN (7n+10;5n+9) ( d thuoc N sao)
=>7n+10 chia hết cho d;5n+9 chia hết cho d
=>35n+50 chia het cho d;35n+63
=>-13 chia hết d
Ma 7n+10 ko chia het cho d => 7n+10/5n+9 la ps toi gian
3 tháng 4 2017
Gọi d là UCLN( 7.n +10, 5.n+9)
=> 7n +10 chia hết d
5n +9 chia hết d
ta có ; 5(7n +10) - 7(5n +9) = 50 - 63 = -13 CHIA HẾT CHO d
Mặt khác : 7n+10 là số lẻ , 5n +9 là số chẵn => phân số đó tối giản
Mình chỉ làm tắt thôi nhé có gì lên lớp hỏi cô giáo
D
1
XO
6 tháng 5 2021
Gọi ƯCLN(2n + 5,3n + 7) = d (d \(\inℤ;d\ne0\))
=> Ta có :\(\hept{\begin{cases}2n+5⋮d\\3n+7⋮d\end{cases}}\Rightarrow\hept{\begin{cases}3\left(2n+5\right)⋮d\\2\left(3n+7\right)⋮d\end{cases}}\Rightarrow\hept{\begin{cases}6n+15⋮d\\6n+14⋮d\end{cases}}\Rightarrow\left(6n+15\right)-\left(6n+14\right)⋮d\)
=> \(1⋮d\Rightarrow d=1\)
