Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với độ dài đường chéo bằng 2a, cạnh SA có độ dài bằng 2a và vuông góc với mặt đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
A. 6 a 2
B. 2 6 a 3
C. 6 a 12
D. 6 a 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
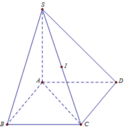
Gọi I là trung điểm của SC. Khi đó I là tâm mặt cầu ngoại
tiếp hình chóp S.ABCD
Ta có: S C = S A 2 + A C 2 = 2 a 2 + 2 a 2 = a 6
Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD là:
R = S C 2 = a 6 2

Đáp án A
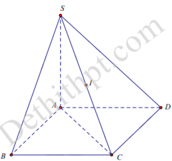
Gọi I là trung điểm SC. Khi đó T là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD
Ta có S C = 2 a 2 + 2 a 2 = a 6
Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD là R = S C 2 = a 6 2

Đáp án D
Theo định lí ba đường vuông góc ta có hai tam giác SBC và SDC lần lượt vuông góc tại B, D. Gọi I là trung điểm của SC thì ta có: IA = IB = ID = SC/2 = IS = IC nên I là tâm mặt cầu ngoại tiếp hình chóp. Bán kính mặt cầu ngoại tiếp hình chóp là 

Đáp án A
Gọi N là trung điểm của MD, khi đó N là tâm đường tròn ngoại tiếp tam giác vuông ADM.
Dựng đường thẳng Δ đi qua N và song song với SA⇒Δ là trục đường tròn ngoại tiếp tam giác ADM.
Dựng mặt phẳng trung trực (P) của SA, P ∩ Δ = I , khi đó I là tâm của mặt cầu ngoại tiếp hình chóp SADM, bán kính R = IA .
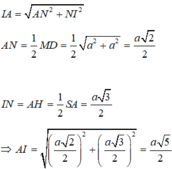
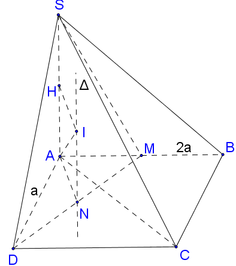

Đáp án C
Từ giả thiết ta có SA ⊥ (ABCD), theo định lí ba đường vuông góc ta có tam giác SBC vuông tại B. Gọi S(B,r) là mặt cầu tâm B cắt SC theo một dây có độ dài 2a/3. Khi đó ta tính được:
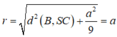

Đáp án C
Gọi O là trung điểm của SD. Ta có: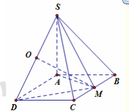
A D = D M = a 2 và A D = 2 a ⇒ A M ⊥ D M
Lại có D M ⊥ S A ⇒ D M ⊥ S A M ⇒ D M ⊥ S M
Vì tam giác SAD vuông tại A nên OS = OD = OA. Tương tự với tam giác SMD nên OS = OD = OM.
Vậy O là tâm mặt cầu ngoại tiếp hình chóp S.ADM. Khi đó R = S D 2 = S A 2 + D A 2 2 = a 6 2 .