Tính giá trị các biểu thức sau: A = 3 4 : 2 3 : 3 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
10 tháng 4 2017
Đúng(0)
Những câu hỏi liên quan
HV
2
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 8 2021
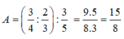
Đề sai rồi, không thể tồn tại x; y sao cho \(\left\{{}\begin{matrix}x+y=3\\xy=5\end{matrix}\right.\) được
Vì \(\left(x+y\right)^2\ge4xy;\forall x;y\) nên \(3^2>4.5\) là vô lý
17 tháng 8 2021
a: \(x^2+y^2=\left(x+y\right)^2-2xy=3^2-2\cdot5=-1\)
b: \(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=3^3-3\cdot3\cdot5=-18\)
HN
1
28 tháng 11 2015
= -{100-99+98-97+.....+2-1}
=-{1x50}= -50
tick mình nhà mình đầu tiên
CM
29 tháng 7 2019
a)
C = 1 − 2 + 3 − 4 + ... + 97 − 98 + 99 − 100 = 1 − 2 + 3 − 4 + ... + 97 − 98 + 99 − 100 = − 1 + − 1 + ... + − 1 + − 1 = − 1.50 = − 50.
b)
B = 1 − 2 − 3 + 4 + 5 − 6 − 7 + ... + 97 − 98 − 99 + 100 = 1 − 2 + − 3 + 4 + 5 − 6 + ... + 97 − 98 + − 99 + 100 = − 1 + 1 + − 1 + ... + − 1 + 1 = − 1 + 1 + − 1 + 1 + ... + − 1 + 1 − 1 = 0 + 0 + ... + 0 − 1 = − 1.
A
1 tháng 3 2018
Bài 1) Chứng minh rằng các biểu thức sau luôn có giá trị âm với mọi giá trị của biến:
a) 9x^2+12x-15
=-(9x^2-12x+4+11)
=-[(3x-2)^2+11]
=-(3x-2)^2 - 11.
Vì (3x-2)^2 không âm với mọi x suy ra -(3x-2)^2 nhỏ hơn hoặc bằng 0 vơi mọi x
Do đó -[(3*x)-2]^2-11 < 0 với mọi giá trị của x.
Hay -9*x^2 + 12*x -15 < 0 với mọi giá trị của x.
b) -5 – (x-1)*(x+2)
= -5-(x^2+x-2)
=-5- (x^2+2x.1/2 +1/4 - 1/4-2)
=-5-[(x-1/2)^2 -9/4]
=-5-(x-1/2)^2 +9/4
=-11/4 - (x-1/2)^2
Vì (x-1/2)^2 không âm với mọi x suy ra -(x-1/2)^2 nhỏ hơn hoặc bằng 0 vơi mọi x
Do đó -11/4 - (x-1/2)^2 < 0 với mọi giá trị của x.
Hay -5 – (x-1)*(x+2) < 0 với mọi giá trị của x.
Bài 2)
a) x^4+x^2+2
Vì x^4 +x^2 lớn hơn hoặc bằng 0 vơi mọi x
suy ra x^4+x^2+2 >=2
Hay x^4+x^2+2 luôn dương với mọi x.
b) (x+3)*(x-11) + 2003
= x^2-8x-33 +2003
=x^2-8x+16b + 1954
=(x-4)^2 + 1954 >=1954
Vậy biểu thức luôn có giá trị dương với mọi giá trị của biến
S
2 tháng 10 2016
a) |x+3/4| >/ 0
|x+3/4| + 1/2 >/ 1/2
MinA= 1/2 <=> x+3/4 =0 hay x= -3/4
b) 2|2x-4/3| >/ 0
2|2x-4/3| -1 >/ -1
MinB = -1 <=> 2|2x-4/3| = 0 hay x=2/3
Bài tiếp théo:
a) -2|x+4| \< 0
-2|x+4| +1 \< 1
MaxA=1 <=> -2|x+4| = 0 hay = -4
b) -3|x-5| \< 0
-3|x-5| + 11/4 \< 11/4
MaxB=11/4 <=> -3|x-5| = 0 hay x=-5
TM
26 tháng 1 2022
1. ĐKXĐ: \(x\ne\pm1\)
2. \(A=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right)\cdot\dfrac{x+1}{2}\)
\(=\dfrac{\left(x+1\right)^2-\left(x-3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{x^2+2x+1-x^2+4x-3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{6x-2}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{2\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x-3}{x-1}\)
3. Tại x = 5, A có giá trị là:
\(\dfrac{5-3}{5-1}=\dfrac{1}{2}\)
4. \(A=\dfrac{x-3}{x-1}\) \(=\dfrac{x-1-3}{x-1}=1-\dfrac{3}{x-1}\)
Để A nguyên => \(3⋮\left(x-1\right)\) hay \(\left(x-1\right)\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}x-1=1\\x-1=-1\\x-1=3\\x-1=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\left(tmđk\right)\\x=0\left(tmđk\right)\\x=4\left(tmđk\right)\\x=-2\left(tmđk\right)\end{matrix}\right.\)
Vậy: A nguyên khi \(x=\left\{2;0;4;-2\right\}\)
Y
26 tháng 6 2023
\(a,\dfrac{3}{2}\times\dfrac{4}{5}\times\dfrac{2}{3}\times\dfrac{15}{4}\\ =\dfrac{3\times4\times2\times15}{2\times5\times3\times4}\\ =\dfrac{3\times4\times2\times5\times3}{2\times5\times3\times4}\\ =3\)
\(b,\dfrac{6}{7}\times\dfrac{5}{8}\times\dfrac{7}{3}\times\dfrac{7}{6}\times\dfrac{8}{5}\\ =\dfrac{6\times5\times7\times7\times8}{7\times8\times3\times6\times5}\\ =\dfrac{7}{3}\)
VN
Võ Ngọc Phương
CTVHS
VIP
26 tháng 6 2023
a) \(\dfrac{3}{2}\times\dfrac{4}{5}\times\dfrac{2}{3}\times\dfrac{15}{4}\)
\(=\left(\dfrac{3}{2}\times\dfrac{2}{3}\right)\times\left(\dfrac{4}{5}\times\dfrac{15}{4}\right)\)
\(=1\times3\)
\(=3\)
b) \(\dfrac{6}{7}\times\dfrac{5}{8}\times\dfrac{7}{3}\times\dfrac{7}{6}\times\dfrac{8}{5}\)
\(=\left(\dfrac{6}{7}\times\dfrac{7}{6}\right)\times\left(\dfrac{5}{8}\times\dfrac{8}{5}\right)\times\dfrac{7}{3}\)
\(=1\times1\times\dfrac{7}{3}\)
\(=\dfrac{7}{3}\)
Chúc bạn học tốt
