Question

[Pham Trong Bach]

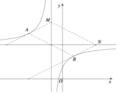
Gọi I là giao điểm hai tiệm cận. viết phương trình tiếp tuyến d của đồ thị hàm số biết d cắt tiệm cận đứng và tiệm cận ngang lần lượt tại A và B thỏa mãn  cos B A I ^ = 5 26 26

A. y = 5x - 2; y = 5x - 3

B. y = 5x - 2; y = 5x + 3

C. y = 5x - 2; y = 5x + 2

D. y = 5x - 3; y = 5x + 2

Answer 1

[Cao Minh Tâm]

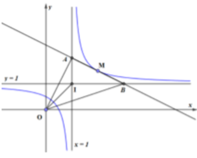
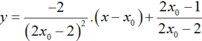
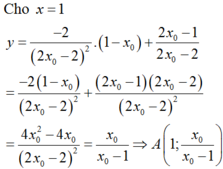
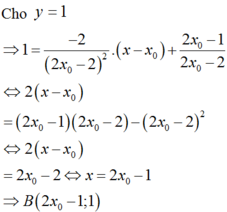
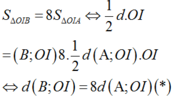
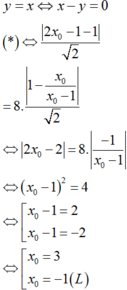
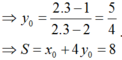
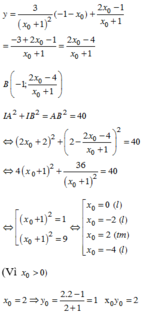
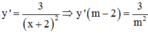
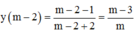
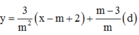
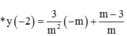
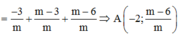
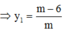
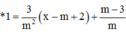
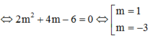
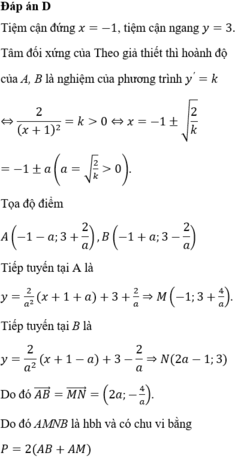
Gọi  M x 0 ; 3 x 0 - 2 x 0 + 1 ∈ C x 0 ≠ - 1

Tiếp tuyến d với (C) tại M có phương trình:  y - 3 x 0 - 2 x 0 + 1 = 5 x 0 + 1 2 x - x 0

Do d cắt tiệm cận đứng, tiệm cận ngang lần lượt tại A, B và ∆ I A B  có  cos B A I ^ = 5 26 26  nên  B A I ^ = 5

Lại có B A I ^  là hệ số góc của tiếp tuyến d mà y ' x 0 = 5 x 0 + 1 2 > 0  nên 

5 x 0 + 1 2 = 5 ⇔ x 0 + 1 2 = 1 ⇔ x 0 = 2 x 0 = 1

Vậy có hai tiếp tuyến thỏa mãn yêu cầu bài toán y = 5x - 2; y = 5x + 2

Đáp án C