Cho hình cầu tâm O bán kính r. Lấy một điểm A trên mặt cầu và gọi ( α ) là mặt phẳng đi qua A sao cho góc giữa OA và ( α ) bằng 30 ° . Đường thẳng đi qua A vuông góc với mặt phẳng ( α ) cắt mặt cầu tại B. Tính độ dài đoạn AB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 3 2019
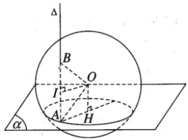
Gọi H là hình chiếu vuông góc của tâm O trên mặt phẳng ( α ). Theo giả thiết ta có ∠ OAH = 30 °
Do đó:
Vậy diện tích của thiết diện tạo bởi ( α ) và hình cầu là:
CM
22 tháng 5 2018
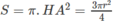
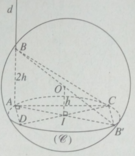
Ta có AH ⊥ DC. Do đó khi CD di động, điểm H luôn luôn nhìn đọan thẳng AI dưới một góc vuông. Vậy tập hợp các điểm H là đường tròn đường kính AI nằm trong mặt phẳng ( α ).
CM
11 tháng 3 2018
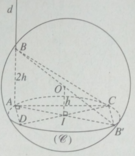
Diện tích tam giác BCD bằng:
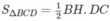
Diện tích này lớn nhất khi AI // CD.
CM
22 tháng 7 2019
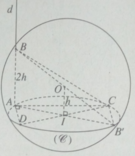
Tam giác ADC vuông tại A nên AD 2 = DC 2 - AC 2 (1)
Tam giác ABC vuông tại A nên BC 2 = AC 2 + AB 2 (2)
Từ (1) và (2) ta suy ra AD 2 + BC 2 = DC 2 + AB 2 (3)
Ta lại có:
AC 2 = DC 2 - AD 2 và BD 2 = AD 2 + AB 2 (4)
DC 2 = 4 r 2 - h 2 , AB 2 = 4 h 2 (5)
Từ (4) và (5) ta có:
AC 2 + BD 2 = DC 2 + AB 2 = 4 r 2 - h 2 + 4 h 2 = 4 r 2 (6)
Từ (3) và (6) ta có: AD 2 + BC 2 = AC 2 + BD 2 (không đổi)
CM
27 tháng 12 2017
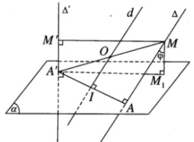
Theo giả thiết ta có: ∠A′M′M = ∠A′AM = ∠A′M1M = 90o
Do đó 5 điểm A, A’, M, M’, M1 cùng thuộc mặt cầu (S) tâm O, với O là trung điểm của A’M và có bán kính r = A′M2
Mặt khác ta có A’M2 = A’A2 + AM2
Trong đó
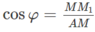
Do đó
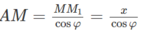
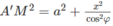
Mặt cầu tâm O có bán kính
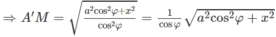
Diện tích của mặt cầu tâm O là:
CM
22 tháng 10 2018
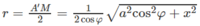
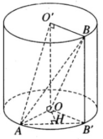
Ta có ( α ) là (ABB’). Vì OO’ // ( α ) nên khoảng cách giữa OO’ và ( α ) bằng khoảng cách từ O đến ( α ). Dựng OH ⊥ AB′ ta có OH ⊥ ( α ).
Vậy khoảng cách cần tìm là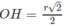 
20 tháng 5 2017
a) Gọi H là hình chiếu vuông góc của tâm O trên mặt phẳng \(\left(\alpha\right)\).
Theo giả thiết ta có \(\widehat{OAH}=30^0\)
Do đó : \(HA=OA\cos30^0=r\dfrac{\sqrt{3}}{2}\)
CM
19 tháng 12 2017
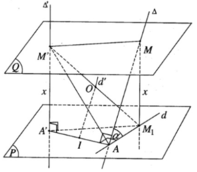
Vì mặt phẳng (P) qua A và vuông góc với Δ′ nên AA’ thuộc (P). Vì M thuộc ∆ mà d là hình chiếu vuông góc của ∆ trên (P) nên M 1 thuộc d. Vì MA ⊥ AA′ ⇒ M 1 A ⊥ AA′
Mặt khác M 1 A ⊥ M′A′ nên ta suy ra M 1 A ⊥ (AA′M′). Do đó M 1 A ⊥ M′A và điểm A thuộc mặt cầu đường kính M’ M 1
Ta có M′A′ ⊥ (P) nên M′A′ ⊥ A′ M 1 , ta suy ra điểm A’ cũng thuộc mặt cầu đường kính M’ M 1
Ta có (Q) // (P) nên ta suy ra
M M 1 ⊥ (Q) mà MM’ thuộc (Q), do đó M 1 M ⊥ MM′
Như vậy 5 điểm A, A’, M, M’, M 1 cùng thuộc mặt cầu (S) có đường kính M’ M 1 . Tâm O của mặt cầu (S) là trung điểm của đoạn M’ M 1
Ta có M ' M 1 2 = M ' A ' 2 + A ' M 1 2 = M ' A ' 2 + A ' A 2 + AM 1 2 = x 2 + a 2 + x 2 cot 2 α vì M M 1 = x
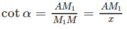
Bán kính r của mặt cầu (S) bằng (M′ M 1 )/2 nên
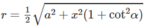
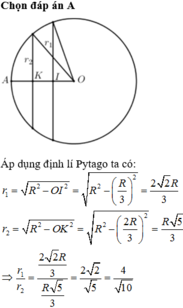
Mặt phẳng (ABO) qua tâm O của hình cầu nên cắt mặt cầu theo đường tròn lớn qua A và B. Gọi I là trung điểm của đoạn AB ta có OI ⊥ AB. Vì AB // OH nên AIOH là hình chữ nhật.
Do đó
Vậy AB = 2AI = r
Chú ý: Có thể nhận xét rằng tam giác OAB cân tại O (OA = OB) và có góc ∠ OAB = 60 ° nên OAB là tam giác đều và suy ra AB = OA = OB = r.