Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
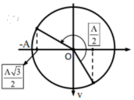
Vẽ vòng tròn lượng giác ta xác định góc quay tương ứng là 60o+90o+60 = 210o
Chọn đáp án A
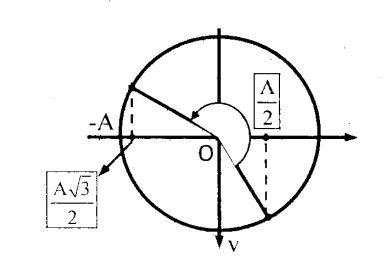
x 1 = 3 = A 2 → x 2 = − 3 2 = − A 3 2
Từ VTLG ta thu được thời gian cần tìm là:
Δ t = T 2 + T 12 → T = 0 , 5 s Δ t = 7 24 s
Chọn C
+ T = 2 π w = 4 s
+ Khoảng thời gian ngắn nhất để con lắc đi từ vị trí có li độ s = 3cm đến li độ cực đại S0 = 6cm: t = T 6 = 4 6 = 2 3 s .
Ban đầu vật ở vị trí có pha ban đầu là -pi/3
Sau 13s, vật quét được góc: \(\varphi=\omega t=4\pi.13=52\pi\left(rad\right)\)
Vì góc quay được chia hết cho 2, nghĩa là sau 13s, vật sẽ quay về vị trí ban đầu có pha là -pi/3
\(\Rightarrow S=45cm=3+7.6=\dfrac{A}{2}+7A\)
Vậy vật quay được góc: \(\varphi=\dfrac{\pi}{3}+4\pi-\dfrac{\pi}{2}=\dfrac{23}{6}\pi\left(rad\right)\)
\(\Rightarrow t=\dfrac{\varphi}{\omega}=\dfrac{23\pi}{6.4\pi}=\dfrac{23}{24}\left(s\right)\)
Chọn D
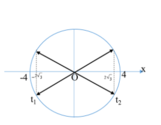
+ T = 2 π w = 2 π 8 π = 0 , 25 s
+ Quãng đường vật đi được là: S = 2 3 + 2 3 = 4 3 cm.
+ Sử dụng vòng tròn ta có thời gian vật đi từ
x1 = - A 3 2 đến x2 = A 3 2 là:
t = t - A 3 / 2 → O + t A 3 / 2 → O = T 6 + T 6 = T 3 = 1 12 s .
+ Tốc độ trung bình: vtb = S: t = 48 3 cm/s.
