Trong một hình tứ diện ta tô màu các đỉnh, trung điểm các cạnh, trọng tâm các mặt và trọng tâm tứ diện. Chọn ngẫu nhiên 4 điểm trong số các điểm đã tô màu. Tính xác suất để 4 điểm được chọn là 4 đỉnh của một hình tứ diện.
A. 188 273
B. 1009 1365
C. 245 273
D. 136 195

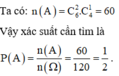
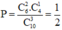

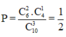
Đáp án A.
Có tất cả 15 điểm được tô màu gồm 4 đỉnh của tứ diện, 6 trung điểm của 6 cạnh, 4 trọng tâm của 4 mặt bên và 1 trọng tâm của tứ diện.
Không gian mẫu là “Chọn ngẫu nhiên 4 trong số 15 điểm đã tô màu”. Số phần tử của không gian mẫu là n Ω = C 15 4 .
Gọi A là biến cố “4 điểm được chọn đồng phẳng”. Suy ra là biến cố “4 điểm được chọn là 4 đỉnh của một hình tứ diện”. Để xác định số kết quả thuận lợi cho biến cố A ta xét các trường hợp sau:
a. 4 điểm cùng thuộc “một mặt bên của tứ diện”
Một mặt bên có 7 điểm được tô màu nên số cách chọn 4 điểm (đồng phẳng) trên một mặt bên là C 7 4 (cách).
Có tất cả 4 mặt bên nên số cách chọn thỏa mãn trường hợp a. là 4. C 7 4 (cách).
b. 4 điểm cùng thuộc mặt phẳng “chứa 1 cạnh của tứ diện và trung điểm của cạnh đối diện:.
Mặt phẳng đó có 7 điểm được tô màu nên số cách chọn 4 điểm (đồng phẳng) trên mỗi mặt là C 7 4 (cách).
Hình tứ diện có 6 cạnh nên có tất cả 6 mặt như thế. Số cách chọn 4 điểm thỏa mãn trường hợp b. là 6 C 7 4 (cách).
c. 4 điểm cùng thuộc mặt phẳng “chứa 1 đỉnh và đường trung bình của tam giác đối diện đỉnh đó”.
Mặt phẳng đó có 5 điểm được tô màu nên số cách chọn 4 điểm (đồng phẳng) trên mỗi mặt là C 5 4 (cách).
Do mỗi mặt bên là một tam giác có 3 đường trung bình, nên mỗi đỉnh có tương ứng 3 mặt phẳng như thế (chứa đỉnh và đường trung bình). Mà tứ diện có 4 đỉnh nên có tất cả 3.4 = 12 mặt phẳng ở trường hợp c.
Vậy số cách chọn thỏa mãn trường hợp c. là 12 C 5 4 (cách).
d. 4 điểm cùng thuộc mặt phẳng “chứa 2 đường nối 2 trung điểm của các cạnh đối diện”.
Có 3 đường nối 2 trung điểm của các cạnh đối diện. Số mặt phẳng được tạo thành từ 2 trong 3 đường đó là C 3 2 (mặt phẳng).
Mỗi mặt phẳng như thế có 5 điểm được tô màu nên số cách chọn 4 điểm (đồng phẳng) là C 5 4 (cách).
Vậy số cách chọn thỏa mãn trường hợp d. là C 3 2 . C 5 4 (cách).
Số kết quả thuận lợi cho biến cố A là n A = 4 C 7 4 + 6 C 7 4 + 12 C 5 4 + C 3 2 . C 5 4 = 425 .
Vậy xác suất cần tính là
P A ¯ = 1 − P A = 1 − n A n Ω = 1 − 425 C 15 4 = 188 173