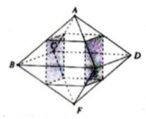
Cho hình bát diện đều ABCDEF cạnh a. Tính theo a thể tích V của khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện (xem hình vẽ)
A. V = a 3 2 .
B. V = a 3 2 4 .
C. V = a 3 2 2 .
D. V = a 3 2 8 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
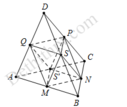
Khối bát diện đều có cạnh là a.
Chia bát diện đều thành hai hình chóp tứ giác đều có tất cả các cạnh bằng a.
Thể tích khối chóp tứ giác đều S.MNPQ là


Đáp án C

Khối bát diện đều có cạnh là a.
Chia bát diện đều thành hai hình chóp tứ giác đều có tất cả các cạnh bằng a.
Thể tích khối chóp tứ giác đều S.MNPQ là
V S . M N P Q = 1 3 d S ; M N P Q . S M N P Q = 1 3 . a 2 − a 2 2 . a 2 = a 3 2 6
Vậy thể tích cần tính là:
V = 2 x V S . M N P Q = 2. a 3 2 6 = a 3 2 3 .
Phương pháp:
Khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện đều ABCDEF (như hình vẽ) là hình hộp chữ nhật.
Cách giải:
Khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện đều ABCDEF là hình hộp chữ nhật có đáy là hình vuông cạnh a 2 ;