Tìm tất cả các giá trị thực của tham số m để bất phương trình m 5 − x + 4 − x = x x + x + 12 có nghiệm.
A. 2 15 − 4 3 ≤ m ≤ 12
B. 2 15 − 4 3 < m < 12
C. m ≤ 12
D. m ≥ 2 15 − 4 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Trường hợp 1: m=0
Bất phương trình sẽ là \(0x^2+3\cdot0\cdot x+0+1>0\)
=>1>0(luôn đúng)
Trường hợp 2: m<>0
\(\text{Δ}=\left(3m\right)^2-4m\left(m+1\right)\)
\(=9m^2-4m^2-4m=5m^2-4m\)
Để phương trình có nghiệm đúng với mọi số thực x thì \(\left\{{}\begin{matrix}m\left(5m-4\right)< 0\\m>0\end{matrix}\right.\Leftrightarrow0< m< \dfrac{4}{5}\)
Vậy: 0<=m<4/5
b: Trường hợp 1: m=4
\(g\left(x\right)=\left(4-4\right)\cdot x^2+\left(2\cdot4-8\right)x+4-5=-1< 0\)(luôn đúng)
Trường hợp 2: m<>4
\(\text{Δ}=\left(2m-8\right)^2-4\left(m-4\right)\left(m-5\right)\)
\(=4m^2-32m+64-4\left(m^2-9m+20\right)\)
\(=4m^2-32m+64-4m^2+36m-80\)
=4m-16
Để bất phương trình luôn âm thì \(\left\{{}\begin{matrix}4m-16< 0\\m-4< 0\end{matrix}\right.\Leftrightarrow m< 4\)
Vậy: m<=4

Chọn D
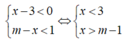
Hệ bất phương trình vô nghiệm khi và chỉ khi m - 1 ≥ 3 hay m ≥ 4


Để bất phương trình luôn có nghiệm thì
\(\left\{{}\begin{matrix}\left(m-1\right)^2-4\cdot1\cdot5< 0\\1>=0\end{matrix}\right.\Leftrightarrow\left(m-1\right)^2< 20\)
\(\Leftrightarrow-2\sqrt{5}+1< x< 2\sqrt{5}+1\)

2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)
Đáp án A
Tập xác định của hàm số: D = 0 ; 4
Ø Xét tử số, đặt g x = x x + x + 12
Em thấy g x > 0 ∀ x ∈ 0 ; 4 g ' x = 3 x 2 x + 1 2 x + 12 > 0 ⇒ g x là hàm dương và đồng biến trên [0;4]
Ø Xét mẫu số, xét h x = 5 − x + 4 − x
Em thấy h x > 0 ∀ x ∈ 0 ; 4 h ' x = − 1 2 5 − x + − 1 2 4 − x < 0
=> h(x) là hàm dương và nghịch biến trên [0;4]
=> 1 h x là hàm đồng biến trên [0;4] ⇒ y = g x . 1 h x là hàm đồng biến trên [0;4]
⇒ maxy = y 4 = 12 ; miny = y 0 = 2 15 − 4 3