Cho hai phương trình x + 2y = 4 và x – y = 1. Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của các phương trình nào.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 12 2019
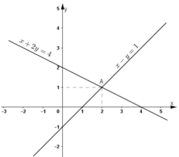
- Vẽ đường thẳng x + 2y = 4.
+ Với x = 0 ⇒ y = 2. Đường thẳng đi qua điểm (0; 2).
+ Với y = 0 ⇒ x = 4. Đường thẳng đi qua điểm (4; 0).
Đường x + 2y = 4 là đường thẳng đi qua điểm (0; 2) và (4; 0).
- Vẽ đường thẳng x – y = 1
+ Với x = 0 ⇒ y = -1. Đường thẳng đi qua điểm (0; -1).
+ Với y = 0 ⇒ x = 1. Đường thẳng đi qua điểm (1; 0).
Đường x – y = 1 là đường thẳng đi qua điểm (0 ; -1) và (1 ; 0).
- Giao điểm của hai đường thẳng là điểm A có tọa độ là (2; 1).
- Ta có A(2; 1) cùng thuộc hai đường thẳng nên nó là nghiệm của cả hai phương trình đã cho.
CM
2 tháng 11 2017
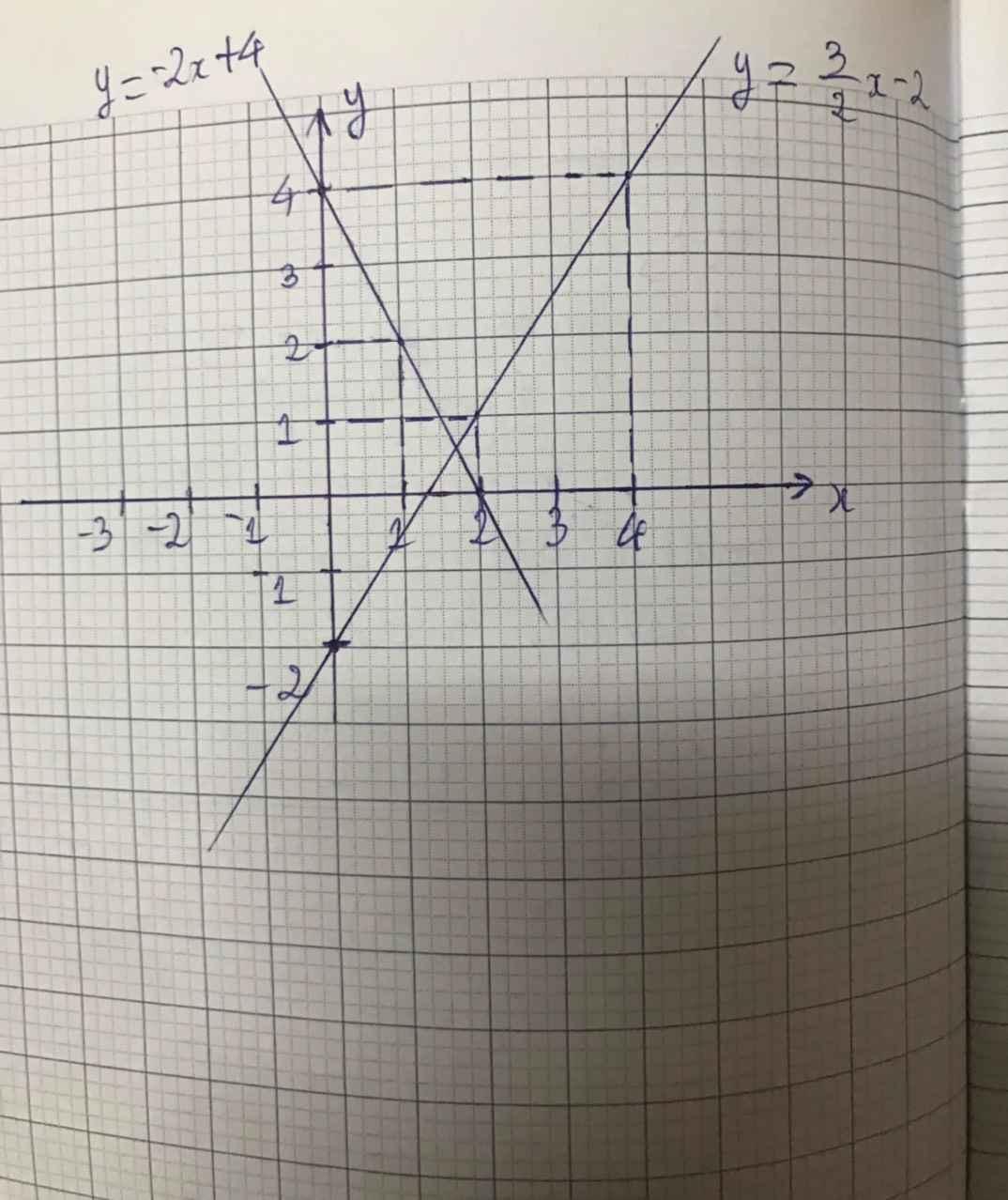
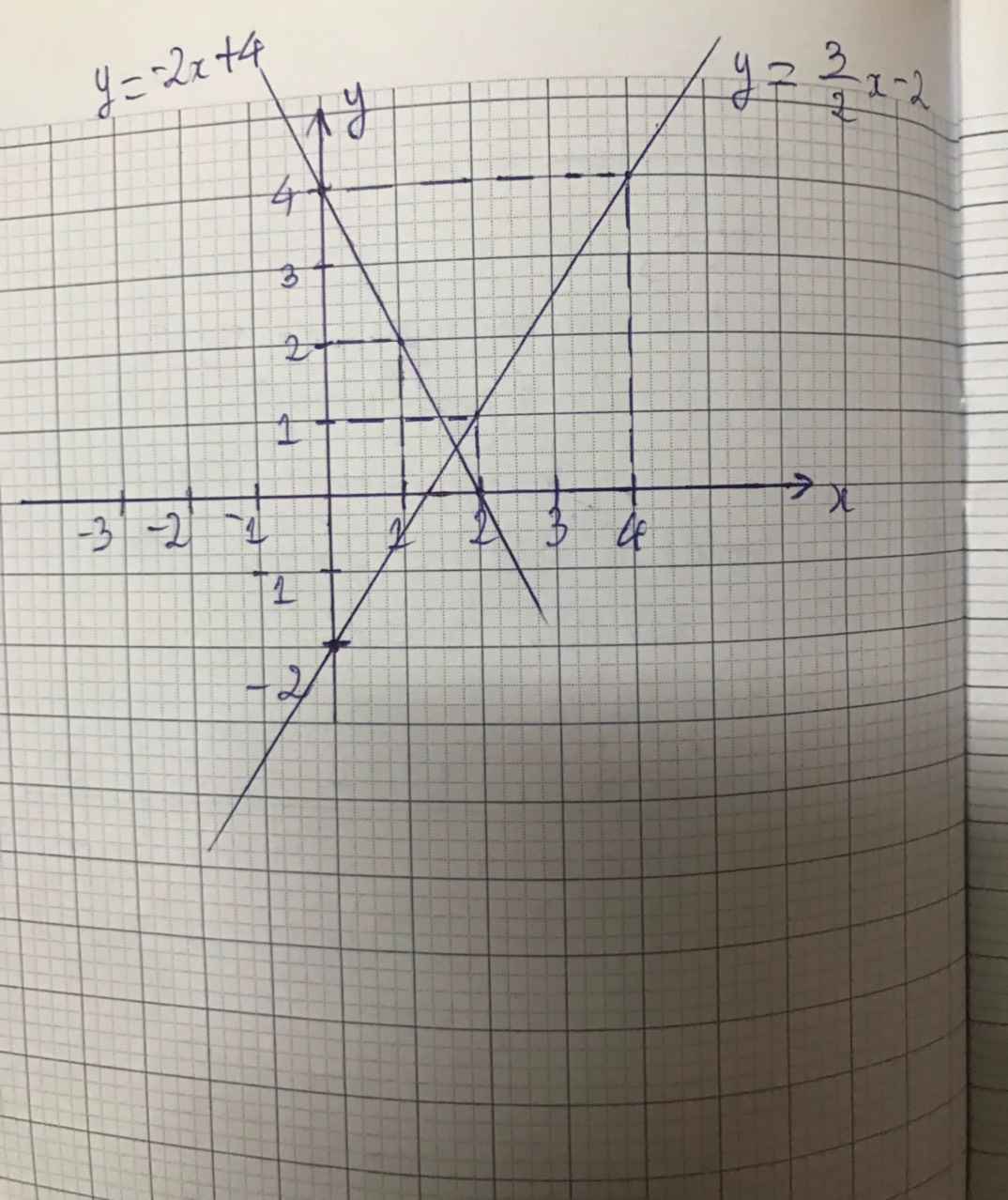
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng (d) : y = -2x + 4.
Chọn x = 0 ⇒ y = 4
Chọn y = 0 ⇒ x = 2.
⇒ (d) đi qua hai điểm (0; 4) và (2; 0).
Đường thẳng biểu diễn tập nghiệm của phương trình (2) là đường thẳng (d’) :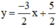 
Chọn x = 0 ⇒ y = 2,5.
Chọn y = 0 ⇒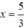 
⇒ (d’) đi qua hai điểm (0; 2,5) và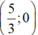 
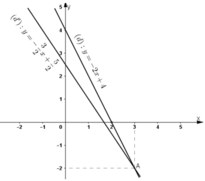
Hai đường thẳng cắt nhau tại A(3; -2).
Vậy (3; -2) là nghiệm chung của hai phương trình (1) và (2)
CM
30 tháng 9 2019
a) + Xét phương trình 2x + y = 4 (1) ⇔ y = -2x + 4
Vậy phương trình (1) có nghiệm tổng quát là (x ; -2x + 4) (x ∈ R).
+ Xét phương trình 3x + 2y = 5 (2) ⇔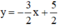 
Vậy phương trình (2) có nghiệm tổng quát là :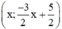 
(x ∈ R).
b) Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng (d) : y = -2x + 4.
Chọn x = 0 ⇒ y = 4
Chọn y = 0 ⇒ x = 2.
⇒ (d) đi qua hai điểm (0; 4) và (2; 0).
Đường thẳng biểu diễn tập nghiệm của phương trình (2) là đường thẳng (d’) :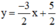 
Chọn x = 0 ⇒ y = 2,5.
Chọn y = 0 ⇒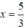 
⇒ (d’) đi qua hai điểm (0; 2,5) và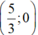 
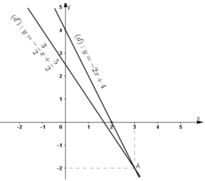
Hai đường thẳng cắt nhau tại A(3; -2).
Vậy (3; -2) là nghiệm chung của hai phương trình (1) và (2).
11 tháng 2 2017
a) . Do đó phương trình có nghiệm dạng tổng quát như sau:
hoặc
b) Vẽ (d1): 2x + y = 4
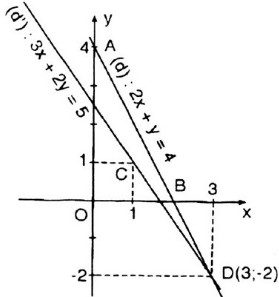
- Cho x = 0 => y = 4 được A(0; 4).
- Cho y = 0 => x = 2 được B(2; 0).
Vẽ (d2): 3x + 2y = 5
- Cho x = 0 => y = 
được C(0; ).
- Cho y = 0 => x = 
được D(; 0).
Hai đường thẳng cắt nhau tại M(3; -2).
Thay x = 3, y = -2 vào từng phương trình ta được:
2 . 3 + (-2) = 4 và 3 . 3 + 2 . (-2) = 5 (thỏa mãn)
Vậy (x = 3; y = -2) là nghiệm chung của các phương trình đã cho.
MT
3 tháng 4 2017
Vẽ đường thẳng x + 2y = 4.
- Cho x = 0 => y = 2 được A(0; 2).
- Cho y = 0 => x = 4 được B(4; 0).
Đường thẳng cần vẽ là đường thẳng qua A, B.
Vẽ đường thẳng x - y = 1.
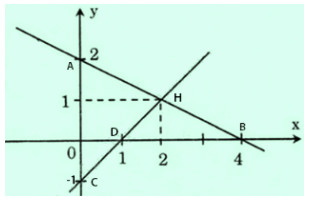
- Cho x = 0 => y = -1 được C(0; -1).
- Cho y = 0 => x = 1 được D(1; 0).
Đường thẳng cần vẽ là đường thẳng qua C, D.
Giao điểm của hai đường thẳng có tọa độ là (2; 1).
Ta có (2; 1) cùng thuộc hai đường thẳng nên nó là nghiệm của cả hai phương trình đã cho.
20 tháng 12 2020
b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)
hay \(-x-4=3x+2\)
\(\Leftrightarrow-x-4-3x-2=0\)
\(\Leftrightarrow-4x-6=0\)
\(\Leftrightarrow-4x=6\)
hay \(x=-\dfrac{3}{2}\)
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được:
\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)
Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)
c) Vì (D2) song song với (D) nên a=-1
hay (D2): y=-x+b
Vì (D2) đi qua điểm B(-2;5)
nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được:
-(-2)+b=5
hay b=5-2=3
Vậy: (D2): y=-x+3
20 tháng 12 2020
b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)
hay \(-x-4=3x+2\)
\(\Leftrightarrow-x-4-3x-2=0\)
\(\Leftrightarrow-4x-6=0\)
\(\Leftrightarrow-4x=6\)
hay \(x=-\dfrac{3}{2}\)
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được:
\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)
Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)
c) Vì (D2) song song với (D) nên a=-1
hay (D2): y=-x+b
Vì (D2) đi qua điểm B(-2;5)
nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được:
-(-2)+b=5
hay b=5-2=3
Vậy: (D2): y=-x+3
- Vẽ đường thẳng x + 2y = 4.
+ Với x = 0 ⇒ y = 2. Đường thẳng đi qua điểm (0; 2).
+ Với y = 0 ⇒ x = 4. Đường thẳng đi qua điểm (4; 0).
Đường x + 2y = 4 là đường thẳng đi qua điểm (0; 2) và (4; 0).
- Vẽ đường thẳng x – y = 1
+ Với x = 0 ⇒ y = -1. Đường thẳng đi qua điểm (0; -1).
+ Với y = 0 ⇒ x = 1. Đường thẳng đi qua điểm (1; 0).
Đường x – y = 1 là đường thẳng đi qua điểm (0 ; -1) và (1 ; 0).
- Giao điểm của hai đường thẳng là điểm A có tọa độ là (2; 1).
- Ta có A(2; 1) cùng thuộc hai đường thẳng nên nó là nghiệm của cả hai phương trình đã cho.