Biểu thức A = 3(sin4x + cos4x) - 2 (sin6x + cos6x) có giá trị bằng:
A. 1
B. 2
C. -1
D. 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 10 2017
a, Ta có: sin 4 x + cos 4 x = sin 2 x + cos 2 x 2 - 2 sin 2 x . cos 2 x = 1 - 2 sin 2 x . cos 2 x
b, Ta có: sin 6 x + cos 6 x = sin 2 x + cos 2 x 3 - 3 sin 2 x cos 2 x sin 2 x + cos 2 x = 1 - 3 sin 2 x cos 2 x
M
14 tháng 6 2020
\(D=\frac{sin4x+sin5x+sin6x}{cos4x+cos5x+cos6x}\)
\(=\frac{\left(sin4x+sin6x\right)+sin5x}{\left(cos4x+cos6x\right)+cos5x}\)
\(=\frac{2sin\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+sin5x}{2cos\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+cos5x}\)
\(=\frac{2sin5x.cos\left(-x\right)+sin5x}{2cos5x.cos\left(-x\right)+cos5x}=\frac{sin5x\left(2.cos\left(-x\right)+1\right)}{cos5x\left(2.cos\left(-x\right)+1\right)}=\frac{sin5x}{cos5x}=tan5x\)
PT
1
CM
30 tháng 8 2019
Chứng minh các biểu thức đã cho không phụ thuộc vào x.
f(x) = 1 ⇒ f′(x) = 0
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
\(P=\dfrac{-2sin5x.sinx-sinx}{2sin5x.cosx+cosx}=\dfrac{-sinx\left(2sin5x+1\right)}{cosx\left(2sin5x+1\right)}=-tanx\)
CM
1 tháng 11 2018
(1) trở thành 4t2 – 2t -6 – m = 0 (2); △ ' = 25 + 4 m .
Để (1) vô nghiệm, ta sẽ tìm m sao cho (1) có nghiệm rồi sau đó phủ định lại.
(1) có nghiệm thì (2) phải có nghiệm thoả t o ∈ - 1 ; 1
Nếu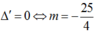 
, (2) có nghiệm kép 
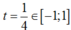nên 
thoả (1) có nghiệm.
Nếu 
, khi đó (2) phải có hai nghiệm phân biệt thoả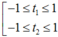 
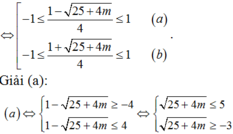
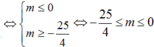
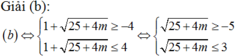
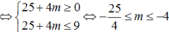
Chọn A.
Ta có:
+ sin4x + cos4x = (sin2x + cos2x)2 - 2sin2x.cos2x = 1 - 2sin2x.cos2x.
+ sin4x + cos4x = 1 - 3sin2x.cos2x.
Do đó
A = 3(1 - 2sin2x.cos2x) - 2(1 - 3sin2x.cos2x) = 1.