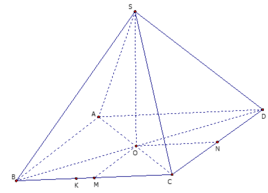
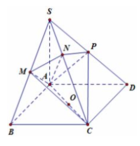
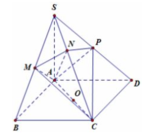
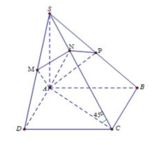
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD. Biết khoảng cách giữa hai đường thẳng BC và SM bằng a 3 4 . Tính thể tích của khối chóp đã cho theo a.
A. a 3 3 4
B. a 3 3 2
C. a 3 3 6
D. a 3 3 12


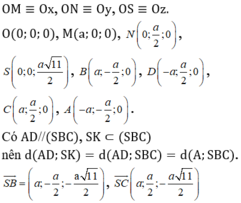

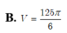


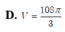

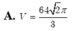
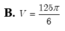
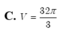
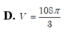



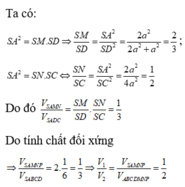
Chọn C
Gọi N là trung điểm của AB => BC // (SMN)
Suy ra d (BC, SM)=d (BC, (SMN))=d (B, (SMN))=d (A, (SMN)).
Dựng AH vuông góc với SN tại H
Lại có, trong tam giác vuông SAN: