Trong không gian Oxyz, viết phương trình mặt phẳng (α) đi qua điểm A ( 1 ; 2 ; - 2 ) , B ( 2 ; - 1 ; 4 ) và vuông góc với ( β ) : x - 2 y - z + 1 = 0 .
A. 15x + 7y + z – 27 = 0
B. 15x – 7y + z + 1 = 0
C. 15x – 7y – z + 1 = 0
D. Đáp án khác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Vì β song song với α nên loại đáp án C và D.
Thử trực tiếp thấy điểm A 1 ; 2 ; 3 thuộc mặt phẳng x − 4 y + z + 4 = 0 .
Do đó đáp án đúng là B.

Chọn C
Gọi giao điểm của Δ và d là B nên ta có: B (3+t;3+3t;2t) ![]()
Vì đường thẳng Δ song song với mặt phẳng (α) nên:
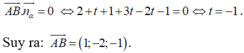
Phương trình đường thẳng Δ đi qua A và nhận 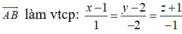

Đáp án C
Gợi A’, B’ C’ hình chiếu của A lên Ox, Oy, Oz. Ta có:
A'(5;0;0), B'(0;4;0), C(0;0;3) => PT ( α ) : x 5 + y 4 + z 3 = 1

Đáp án C.
Mặt phẳng α nhận O M → ; u Ox → là một VTPT.
Mà O M → = 1 ; 0 ; − 1 u O x → = 1 ; 0 ; 0
⇒ O M → ; u Ox → = 0 ; − 1 ; 0 .
Kết hợp với α đi qua M(1;0;-1)
⇒ α : − y − 0 = 0 ⇔ y = 0.
Chọn A.
Mặt phẳng chứa A, B và vuông góc với (β) nên (α) có một vectơ pháp tuyến là: