Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D.
Phương pháp:
Gọi z = a + b i , sử dụng công thức tính môđun của số phức.
Cách giải:
Giả sử z = x + y i , x , y ∈ R
Theo đề bài ta có:
z + 3 − 4 i = 5 ⇔ x + 3 2 + y − 4 2 = 5 ⇔ x + 3 2 + y − 4 2 = 25
Vậy, tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là đường tròn tâm I − 3 ; 4 , R = 5.
Đáp án C
Đặt 
Số phức w được biểu diễn bởi điểm M (x;y).
Ta có:
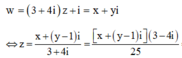
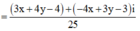
=> |z| =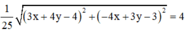 
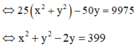
Vậy số phức w được biểu diễn bởi đường tròn tâm I (0;1), bán kính R = 20 và có phương trình: 
Đáp án C
Đặt w = x + yi , x ; y ∈ ℝ . Số phức w được biểu diễn bởi điểm M(x;y).
Ta có:
w = 3 + 4 i z + i = x + yi
⇔ z = x + y − 1 i 3 + 4 i = x + y − 1 i 3 − 4 i 25 = 3 x + 4 y − 4 + − 4 x + 3 y − 3 i 25
⇒ z = 1 25 3 x + 4 y − 4 2 + − 4 x + 3 y − 3 2 = 4
⇔ 3 x + 4 y − 4 2 + − 4 x + 3 y − 3 2 = 100 2
⇔ 3 x + 4 y 2 + − 4 x + 3 y 2 − 8 3 x + 4 y + 16 − 6 − 4 x + 3 y + 9 = 10000
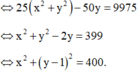
Vậy số phức w được biểu diễn bởi đường tròn tâm I(0;1), bán kính R = 20 và có phương trình: x 2 + y − 1 2 = 400 .
Chọn D