Cho ba lực 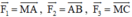 cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của hai lực F1, F2 đều là 100N và ∠AMB = 60o. Tìm cường độ và hướng của lực F3.
cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của hai lực F1, F2 đều là 100N và ∠AMB = 60o. Tìm cường độ và hướng của lực F3.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A
Để vật đứng yên, ba lực đó phải thoả mãn hợp lực bằng không, tức là F 1 , F 2 cùng chiều nhau và F 3 ngược chiều với hai lực trên.

Để vật đứng yên, ba lực đó phải thỏa mãn F 1 → , F 3 → cùng chiều nhau và F 2 ⇀ ngược chiều với hai lực trên. Khi đó hợp lực của chúng F = F 1 + F 3 - F 2 = 0
⇒ Đáp án B

C
Để vật đứng yên, ba lực đó phải thoả mãn F 2 , F 3 cùng chiều nhau và F 1 ngược chiều với hai lực trên.

B
Ba lực cùng phưomg có cường độ lần lượt là F 1 = 20N, F 2 = 60N và F3 = 40N tác dụng vào một vật. Để vật đứng yên, ba lực đó phải thoả mãn là F 1 , F 3 cùng chiều nhau và F 2 ngược chiều với hai lực trên.
Khi đó hợp lực của chúng F = F 1 + F 3 – F 2 = 0.

a) Do vật đứng yên nên \(\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{0}\Leftrightarrow\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\).
Suy ra M là trọng tâm tam giác ABC.
Gọi O là trung điểm của AB. Theo quy tắc trung điểm ta có:
\(\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MO}=\overrightarrow{ME}\).
Do tam giác MAB cân tại M và \(\overrightarrow{AMB}=60^o\) nên tam giác MAB đều và \(MO\perp AB\).
Áp dụng định lý Pi-ta-go trong tam giác MOB ta có:
\(MO=\sqrt{MA^2-OA^2}=\sqrt{100^2-50^2}=50\sqrt{3}\).
Suy ra: \(ME=2MO=2.50\sqrt{3}=100\sqrt{3}\).
b)
\(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\Leftrightarrow\overrightarrow{MC}=-\left(\overrightarrow{MA}+\overrightarrow{MB}\right)\)
Vì vậy véc tơ \(\overrightarrow{MC}\) ngược hướng với véc tơ \(\overrightarrow{MA}+\overrightarrow{MB}\).
Theo kết quả câu a ta suy ra: \(\left|\overrightarrow{ME}\right|=100\sqrt{3}\).
Nên véc tơ \(\overrightarrow{MC}\) có độ dài \(100\sqrt{3}\) và ngược hướng với véc tơ \(\overrightarrow{MA}+\overrightarrow{MB}\).
Vì vậy lực \(\overrightarrow{F_3}\) có cường độ \(100\sqrt{3}N\) và ngược hướng với véc tơ \(\overrightarrow{MA}+\overrightarrow{MB}\).
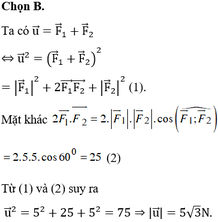
Ta biểu diễn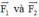 bằng hai vec tơ
bằng hai vec tơ 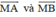 như hình vẽ.
như hình vẽ.
Khi đó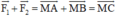 (C là đỉnh còn lại của hình bình hành MACB).
(C là đỉnh còn lại của hình bình hành MACB).
+ Tính MC : Gọi I là trung điểm của AB ⇒ I là trung điểm của MC.
Δ MAB có MA = MB = 100 và góc AMB = 60º nên là tam giác đều
⇒ đường cao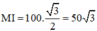
⇒ MC = 2.MI = 100√3.
Vec tơ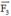 là vec tơ đối của
là vec tơ đối của 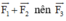 có hướng ngược với
có hướng ngược với  và có cường độ bằng 100√3N.
và có cường độ bằng 100√3N.