Một vật rắn phẳng, mỏng có dạng là một tam giác đều ABC, mỗi cạnh là a = 20 cm. Người ta tác dụng vào vật một ngẫu lực nằm trong mặt phẳng của tam giác. Các lực có độ lớn là 8 N và đặt vào hai đỉnh A và B. Tính momen của ngẫu lực trong các trường hợp sau đây : Các lực song song với cạnh AC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


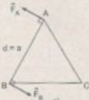
Áp dụng công thức tính momen ngẫu lực M = F.d vào các phần ta được
M = F.d = F.a = 8.0,2 = 1,6 N.m

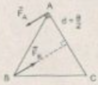
Áp dụng công thức tính momen ngẫu lực M = F.d vào các phần ta được
M = F.d = F.a/2 = 8.0,1 = 0,8 N.m

Đáp án: A
Vì các đường sức từ vuông góc với mặt phẳng của khung dây nên:
Lực từ tác dụng lên cạnh MN có độ lớn là:
F N M = B.I.MN
Lực từ tác dụng lên cạnh NP có độ lớn là:
F N P = B.I.NP
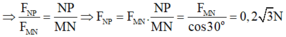
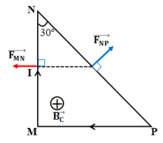
Lực từ tác dụng lên các cạnh hướng ra ngoài khung, nên các góc giữa hai lực là 150 0 .

Đáp án A
Vì các đường sức từ vuông góc với mặt phẳng của khung dây nên:
Lực từ tác dụng lên cạnh MN có độ lớn là:
FMN = B.I.MN
Lực từ tác dụng lên cạnh NP có độ lớn là:
FNP = B.I.NP

Lực từ tác dụng lên các cạnh hướng ra ngoài khung, nên các góc giữa hai lực là 150o.

1/ \(M=F.d=F.a=8.0,2=1,6\left(N.m\right)\)
2/ \(M=F.\frac{a}{2}=8.0,1=0,8\left(N.m\right)\)
3/ => \(d=BH=\sqrt{a^2-\frac{a^2}{4}}=\frac{\sqrt{3}}{4}.0,2=\frac{\sqrt{3}}{20}\left(m\right)\)
\(\Rightarrow M=F.d=\frac{8.\sqrt{3}}{20}=\frac{2\sqrt{3}}{5}\left(N.m\right)\)
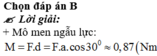
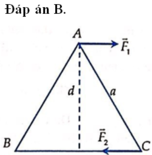


Áp dụng công thức tính momen ngẫu lực M = F.d vào các phần ta được
M = F.d = F.a 3 /2 = 8.0,1 3 /2 = 1,38 N.m