Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm A ( 1 ; 0 ; - 2 ) và có vectơ pháp tuyến n → 1 ; - 1 ; 2 .
A. x - y + 2z – 3 = 0
B. x – y + 2z + 3 = 0
C. x - 2z + 3 = 0
D. x + 2z – 3 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 9 2019
Chọn C.
Mặt phẳng (P) song song với mặt phẳng (Q):2x - 3z + 1 = 0 nên mặt phẳng (P) có phương trình dạng: 2x - 3z + D = 0 (D ≠ 1).
Mặt phẳng (P) đi qua điểm M nên thay tọa độ điểm vào phương trình mặt phẳng (P) ta được:
2.0 - 3.3 + D = 0 ⇔ D = 9 (thỏa mãn D ≠ 1).
Vậy phương trình mặt phẳng (P) là: 2x - 3z + 9 = 0.
CM
8 tháng 2 2019
Chọn B
Mặt phẳng (P) song song với mặt phẳng (Q): 2x – 3z + 1 = 0 nên mặt phẳng (P) có phương trình dạng: 
.
Mặt phẳng (P) đi qua điểm M(0;1;3) nên thay tọa độ điểm vào phương trình mặt phẳng (P) Ta được: 2.0 -3.3 + D = 0 ⇔ D = 9 (thỏa mãn D ≠ 1).
Vậy phương trình mặt phẳng (P) là: 2x – 3z + 9 = 0.
CM
29 tháng 1 2019
Chọn B.
Mặt phẳng (P) đi qua điểm A(1;0;-2) và có vectơ pháp tuyến n → 1 ; - 1 ; 2 có phương trình là:
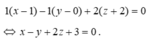
Vậy phương trình mặt phẳng (P) là: x - y + 2z + 3 = 0.
CM
13 tháng 1 2018
Chọn B.
Mặt phẳng (P) đi qua điểm A(1;0;-2) và có vectơ pháp tuyến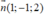 
có phương trình là:
1(x - 1) - 1(y - 0) + 2(z + 2) = 0 ⇔ x - y + 2z + 3 = 0.
Vậy phương trình mặt phẳng (P) là: x- y + 2z + 3 = 0.
CM
18 tháng 2 2017
Chọn C
Phương trình mặt phẳng (P) qua A(1;-2;3), vecto pháp tuyến n → 2 ; - 1 ; - 2
2(x - 1) – 1.(y + 2) – 2.(z – 3) = 0 hay 2x - y – 2z + 2 = 0
CM
5 tháng 8 2018
Chọn D.
Ta có: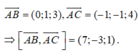
Gọi n → là một vectơ pháp tuyến của mặt phẳng (ABC) ta có
ta được phương trình mặt phẳng (ABC) là:
CM
16 tháng 7 2017
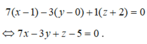
Đáp án C
Ta có n P → 1 ; 0 ; 0 ; n Q → 0 ; 1 ; − 1 suy ra n → = n P → ; n Q → = 0 ; 1 ; 1
Suy ra phương trình mặt phẳng cần tìm là: y + z − 5 = 0
Chọn B.
Mặt phẳng (P) đi qua điểm A(1;0;-2) và có vectơ pháp tuyến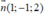
có phương trình là:
1(x - 1) - 1(y - 0) + 2(z + 2) = 0 ⇔ x - y + 2z + 3 = 0.
Vậy phương trình mặt phẳng (P) là: x- y + 2z + 3 = 0.