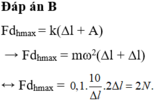1. Một lò xo có độ cứng k=100N/m và có chiều dài tự nhiên là 10cm. Giữ một đầu lò xo cố định, tác dụng vào đầu kiamột lực kéo 5N. Bỏ qua khối lượng lò xo.a. Cho biết độ lớn của lực đàn hồi của lò xo.b...

D

duong ^^

7 tháng 11 2021

1. Một lò xo có độ cứng k=100N/m và có chiều dài tự nhiên là 10cm. Giữ một đầu lò xo cố định, tác dụng vào đầu kiamột lực kéo 5N. Bỏ qua khối lượng lò xo.a. Cho biết độ lớn của lực đàn hồi của lò xo.b. Tính độ biến dạng của lò xo.c. Muốn lò xo dãn thêm 2cm nữa thì phải tăng lực kéo lên bao nhiêu...

Đọc tiếp

#Vật lý lớp 10

0

D

duong ^^

7 tháng 11 2021

1. Một lò xo có độ cứng k=100N/m và có chiều dài tự nhiên là 10cm. Giữ một đầu lò xo cố định, tác dụng vào đầu kiamột lực kéo 5N. Bỏ qua khối lượng lò xo.a. Cho biết độ lớn của lực đàn hồi của lò xo.b. Tính độ biến dạng của lò xo.c. Muốn lò xo dãn thêm 2cm nữa thì phải tăng lực kéo lên bao nhiêu...

Đọc tiếp

#Vật lý lớp 10

1

NT

nguyễn thị hương giang

7 tháng 11 2021

a)Độ lớn của lực đàn hồi: \(F_{đh}=5N\)

b)Độ biến dạng của lò xo: \(\Delta l=\dfrac{F_{đh}}{k}=\dfrac{5}{100}=0,05m=5cm\)

c)Để lò xo dãn thêm 2cm tức \(\Delta l'=2+5=7cm=0,07m\)

Lực đàn hồi lúc này: \(F'_{đh}=0,07\cdot100=7N\)

Cần tăng lực kéo thêm: \(\Delta F=7-5=2N\)

Đúng(3)

VL

Vật lý 10

29 tháng 11 2021

1 lò xo có độ cứng k=100n/m đầu trên giữ cố định.Treo 1 vật có khối lượng m = 500g vào đầu dưới của lò xo thì lực đàn hồi của lò xo và độ giãn của lò xo là bao nhiêu?Biết g = 10m/s2

#Vật lý lớp 10

2

TK

trương khoa

29 tháng 11 2021

m =500 g=0,5 kg

Lực đàn hồi của lò xo là

\(F_{đh}=P=mg=0,5\cdot10=5\left(N\right)\)

Độ giãn của lò xo là

\(\left|\Delta l\right|=\dfrac{F_{đh}}{k}=\dfrac{5}{100}=0,05\left(m\right)=5\left(cm\right)\)

Đúng(2)

N

nthv_.

29 tháng 11 2021

\(500g=0,5kg\)

\(F_{danhoi}=P=mg=0,5\cdot10=5\left(N\right)\)

\(\Delta l=\dfrac{mg}{k}=\dfrac{0,5\cdot10}{100}=0,05m=5cm\)

Đúng(1)

PQ

phương quỳnh

27 tháng 12 2021

1. Một lò xo có độ cứng k = 100N/m, lò xo được giữ cố định tại một đầu, người ta tác dụng vào đầu còn lại một lực kéo F = 5N. Độ biến dạng của lò xo là:A. 5cm. B. 2cm. C. 0,1m. D. 1cm. 2. Tầm xa của một vật ném theo phương ngang là 30m, thời gian rơi là 3s. Vận tốc ban đầu của vật:A. 3 m/s. B. 9...

Đọc tiếp

#Vật lý lớp 10

1

NT

nguyễn thị hương giang

27 tháng 12 2021

Câu 1.

Độ biến dạng của lò xo:

\(\Delta l=\dfrac{F_{đh}}{k}=\dfrac{5}{100}=0,05m=5cm\)

Chọn A.

Câu 2.

Vận tốc ban đầu vật:

\(L=v_0\cdot t\Rightarrow v_0=\dfrac{L}{t}=\dfrac{30}{3}=10\)m/s

Chọn C

Câu 3.

Ta có: \(x_0=10km;v_0=40\)km/h

Phương trình chuyển động:

\(x=x_0+v_0t+\dfrac{1}{2}at^2=10+40t+\dfrac{1}{2}\cdot0\cdot t^2=10+40t\left(km\right)\)

Chọn B

Đúng(1)

PQ

phương quỳnh

27 tháng 12 2021

Em cảm ơn ạ!

Đúng(0)

HD

Hoàng Đức Long

23 tháng 8 2019

Một lò xo có chiều dài tự nhiên 10cm và có độ cứng 40N/m. Giữ cố định một đầu và tác dụng vào đầu kia một lực 1N để nén lò xo. Chiều dài của lò xo khi bị nén là:

A. 5cm

B. 15cm

C. 10cm

D. 7,5cm

#Vật lý lớp 10

1

VT

Vũ Thành Nam

23 tháng 8 2019

Chọn đáp án D

Ta có: F = k.Δl độ biến dạng của lò xo là:

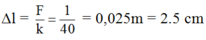
Chiều dài của lò xo khi bị nén là:

l = l₀ – Δl = 10 – 2,5 = 7,5 cm.

Đúng(0)

HD

Hoàng Đức Long

20 tháng 10 2019

Một con lắc lò xo gồm một lò xo nhẹ có độ cứng K, cố định một đầu của lò xo, đầu còn lại của lò xo treo một vật nhỏ có khối lượng m=0,1kg. Lấy g=10m/s2. Giữ vật ở vị trí lò xo không biến dạng rồi thả nhẹ cho vật dao động. Bỏ qua mọi ma sát và lực cản. Trong quá trình dao động của vật, độ lớn cực đại của lực đàn hồi lò xo là A. 3 N B. 2 N C. 4 N D. 1...

Đọc tiếp

#Vật lý lớp 12

1

VT

Vũ Thành Nam

20 tháng 10 2019

Đáp án B

Fd_hmax= k(∆l + A) → Fd_hmax = mω²(∆l + ∆l)

↔ Fd_hmax =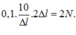

Đúng(0)

HD

Hoàng Đức Long

1 tháng 6 2017

Một con lắc lò xo gồm một lò xo nhẹ có độ cứng K, cố định một đầu của lò xo, đầu còn lại của lò xo treo một vật nhỏ có khối lượng m=0,1kg. Lấy g=10m/ s 2 . Giữ vật ở vị trí lò xo không biến dạng rồi thả nhẹ cho vật dao động. Bỏ qua mọi ma sát và lực cản. Trong quá trình dao động của vật, độ lớn cực đại của lực đàn hồi lò xo là A. 3 N B. 2 N C. 4 N D. 1...

Đọc tiếp

#Mẫu giáo

1

VT

Vũ Thành Nam

1 tháng 6 2017

Đúng(0)

HD

Hoàng Đức Long

15 tháng 9 2019

Lò xo có chiều dài tự nhiên 10cm và độ cứng 40N/m. Giữ cố định một đầu và tác dụng vào đầu kia một lực 1,0N để nén lò xo. Khi ấy chiều dài của lò xo bằng bao nhiêu?

A. 2,5cm

B. 12,5cm

C. 7,5cm

D. 9,75cm

#Vật lý lớp 10

1

VT

Vũ Thành Nam

15 tháng 9 2019

Chọn đáp án C

Lò xo bị nén lại nên ℓ_o > ℓ

Áp dụng:

F = k∆ℓ = k(ℓ_o - ℓ)

→ 1 = 40(0,1 - ℓ)

→ ℓ = 0,075 m = 7,5 cm.

Đúng(0)

HD

Hoàng Đức Long

16 tháng 10 2017

Một lò xo có chiều dài tự nhiên 10 cm và có độ cứng 40 N/m. Giữ cố định một đầu và tác dụng vào đầu kia một lực 1 N để nén lò xo. Chiều dài của lò xo khi bị nén là

A. 5 cm.

B. 15 cm.

C. 10 cm.

D. 7,5 cm.

#Vật lý lớp 10

1

VT

Vũ Thành Nam

16 tháng 10 2017

Đáp án D

Đúng(0)

HD

Hoàng Đức Long

30 tháng 1 2019

Một lò xo có chiều dài tự nhiên 10 cm và có độ cứng 40 N/m. Giữ cố định một đầu và tác dụng vào đầu kia một lực 1 N để nén lò xo. Chiều dài của lò xo khi bị nén là

A. 5 cm.

B. 15 cm.

C. 10 cm.

D. 7,5 cm.

#Vật lý lớp 10

1

VT

Vũ Thành Nam

30 tháng 1 2019

Chọn D.

Ta có: F = k.Δℓ độ biến dạng của lò xo là 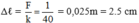Đề kiểm tra 45 phút Vật Lí 10 Học kì 1 có đáp án (Đề 4)

Chiều dài của lò xo khi bị nén là ℓ = ℓ0 – Δℓ = 10 – 2,5 = 7,5 cm.

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP