Tìm hệ số lớn nhất trong khai triển nhị thức Newton của P x = 1 + 2 x 12
A. 126700
B. 126730
C. 126720
D. 126710
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
24 tháng 7 2018
Đúng(0)
Những câu hỏi liên quan
CM
11 tháng 7 2019
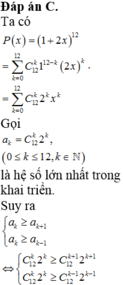
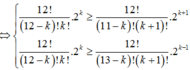
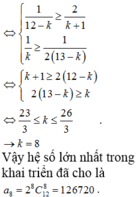
Đáp án C
Ta có P ( x ) = 1 + 2 x 12 = ∑ k = 0 12 C 12 k 1 12 - k = ∑ k = 0 12 C 12 k 2 k x k .
Gọi a k = C 12 K 2 K , 0 ≤ k ≤ 12 , k ∈ ℕ là hệ số lớn nhất trong khai triển.
Suy ra a k ≥ a k + 1 a k ≥ a k - 1 ⇔ c 12 k 2 k ≥ c 12 k + 1 2 k + 1 c 12 k 2 k ≥ c 12 k - 1 2 k - 1
⇔ 12 ! 12 - k ! k ! . 2 k ≥ 12 ! 11 - k ! k + 1 ! . 2 k + 1 12 ! 12 - k ! k ! . 2 k ≥ 12 ! 13 - k ! k + 1 ! . 2 k - 1 ⇔ 1 12 - k ≥ 2 k + 1 1 k ≥ 1 2 13 - k
Vậy hệ số lớn nhất trong khai triển đã cho là a 8 = 2 8 c 12 8 = 126720 .
CM
9 tháng 12 2018
Đáp án A.
Ta có A n 5 ≤ 18 A n - 2 4 ⇔ n ≥ 6 n ! n - 5 ! ≤ 18 . n - 2 ! n - 6 ! ⇔ n ≥ 6 n n - 1 n - 5 ≤ 18 ⇔ 9 ≤ n ≤ 10 → n = 10 .
Với n = 10, xứt khai triển nhị thức
2 x + 1 x x 10 = ∑ k = 10 10 C 10 k . 2 x 10 - k . 1 x 5 x = ∑ k = 0 10 C 10 k . 2 10 - k . x 10 - 6 k 5 .
Hệ số của x 4 ứng với 10 - 6 k 5 = 4 ⇔ k = 5 . Vậy hệ số cần tìm là C 10 5 . 2 5 = 8064 .
