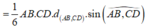Cho khối trụ (T), AB và CD lần lượt là hai đường kính trên hai mặt đáy của (T). Biết góc giữa AB và CD là 30°, AB = 6 và thể tích khối ABCD là 30. Khi đó thể tích khối trụ (T) là:
A . 90 π 3 270 c m 3
B . 30 π c m 3
C . 90 π c m 3
D . 45 π c m 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
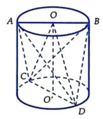
Ta có
V A B C D = 1 6 A B . C D . d A B , C D = sin A B , C D ⏜ ⇒ 30 = 1 6 6 2 . h . sin 30 ° ⇔ h = 10 c m ⇒ V T = πr 2 h = π . 3 2 . 10 = 90 π cm 3

Đáp án B
Giả sử hình vuông ABCD có độ dài cạnh a.
Kẻ các đường sinh AH,BK ta có
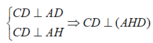
![]()
Theo pitago ta có
![]()
![]()
![]()
![]()


Do đó bán kính đường tròn \(\left(S\right)\cap\left(S'\right)\) bằng \(\dfrac{10\sqrt{41}}{41}a\)
Đáp án C.
Ta có