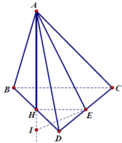
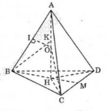
Cho tứ diện ABCD có đáy BCD là tam giác đều, trọng tâm G. ∆ là đường thẳng qua G và vuông góc với (BCD). A chạy trên ∆ sao cho mặt câu ngoại tiếp ABCD có thể tích nhỏ nhất. Khi đó thể tích khối ABCD là:
A . a 3 12
B . a 3 2 12
C . a 3 3 12
D . a 3 3 6


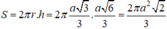
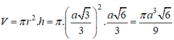

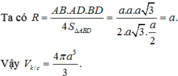
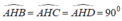
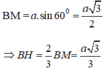
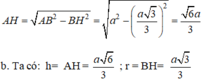
Đáp án A.
Gọi I là tâm mặt cầu ngoại tiếp ABCD => I ∈ ∆ và IA = IB = R
=> Thể tích mặt cầu ngoại tiếp ABCD nhỏ nhất ⇔ IB nhỏ nhất