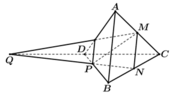
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC, P là điểm thuộc DB sao cho PB = 2PD. Gọi Q là giao điểm của CD với mặt phẳng (MNP). Giao tuyến của hai mặt phẳng (MNP) và (ACD) là:
A. MP
B. NQ
C. MQ
D. AP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BT
6 tháng 6 2017
a) Gọi \(NP\cap CD=K\).
Do \(K\in NP\) nên \(K\in\left(MNP\right)\). Vậy K là giao điểm của CD và (MNP).
b) Do \(M\in AC\) nên \(M\in\left(MNP\right)\cap\left(ACD\right)\).
Và K là giao điểm của CD và (MNP) nên \(K\in\left(MNP\right)\cap\left(ACD\right)\).
Vì vậy MK là giao tuyến của (MNP) và (ACD).
CM
17 tháng 6 2017
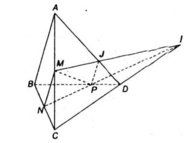
a) Ta có:
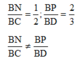
⇒ NP và CD không song song với nhau.
Gọi giao điểm NP và CD là I.
I ∈ NP ⇒ I ∈ (MNP).
Mà I ∈ CD
Vậy I ∈ CD ∩ (MNP)
b) Trong mặt phẳng (ACD) thì AD và MI cắt nhau tại điểm J:
J ∈ AD ⇒ J ∈ (ACD)
J ∈ MI ⇒ J ∈ (MNP)
Vậy J là một điểm chung của hai mặt phẳng (ACD) và (MNP).
Ta đã có M là một điểm chung của hai mặt phẳng (ACD) và (MNP).
Vậy MJ = (ACD) ∩ (MNP).
CM
16 tháng 4 2018
Ta có M là điểm chung thứ nhất.
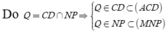
=> Q là điểm chung thứ hai.
Vậy 
Chọn B.
(MNP) ∩ (ACD) = (MNQ) ∩ (ACD) = MQ.
Đáp án C