Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
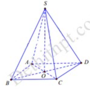
Kí hiệu như hình vẽ với S O ⊥ A B C D và tứ giác ABCD là hình vuông.
Ta có V = 1 3 S O . S A B C D = 1 3 S O . A B 2
Thể tích mới V ' = 1 3 . 1 2 S O . 3 A B 2 = 9 2 V
Đáp án A
Diện tích đáy tăng lên 9 lần và độ dài đường cao xuống hai lần. Khi đó thể tích khối chóp mới là 9 2 V
Chọn D.
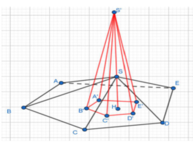
Ta có công thức tính thể tích khối chóp là V = 1 3 S . h . Hai đa giác đồng dạng với nhau nên S S ' . A ' B ' C ' D ' E ' = 1 9 S S . A B C D E . Chiều cao của hình chóp S'.A'B'C'D'E' tăng lên 3 lần nên ta có:
Do đó tỉ số thể tích V ' V = 1 3
Đáp án A
Khi độ dài cạnh đáy tăng lên 2 lần thì diện tích đáy tăng lên 4 lần.
⇒ Thể tích khối chóp tăng lên 4 lần.
Chọn A.
Thể tích hình chóp: 
Khi độ dài cạnh đáy tăng lên 2 lần thì diện tích đáy tăng lên 4 lần.
⇒ Thể tích khối chóp tăng lên 4 lần.
