Cho hình hộp chữ nhật ABCD.A'B'C'D' có diện tích các mặt ABCD, BCC'B', CDD'C' lần lượt là 2a2, 3a2, 6a2. Tính thể tích khối hộp chữ nhật ABCD.A'B'C'D'.
A. 36a3
B. 6a3
C. 36a6
D. 6a2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi độ dài 3 chiều của hình hộp lần lượt là x;y;z . ta có: x y = 2 a 2 y z = 3 a 2 ⇒ x y z = 6 a 3 z x = 6 a 2
Thể tích khối tứ diện là: V = x y z = 6 a 3

Đáp án B
Thể tích khối cầu ngoại tiếp tứ diện ABCD’ chính là thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’. Khi đó, bán kính khối cầu ngoại tiếp là R = A C ' 2 .
Ta có V = 4 3 πR 3 = 4 3 π . AC ' 3 8 = 9 2 πa 3 ⇒ AC ' 3 = 27 a 3 ⇒ AC ' = 3 a .
Mặt khác A C ' 2 = A B 2 + A D 2 + A A ' 2 ⇒ A D 2 = ( 3 a 2 ) - a 2 - ( 2 a ) 2 = 4 a 2 ⇒ A D = 2 a .
Vậy thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là V = A A ' . A B . A D = a . 2 a . 2 a = 4 a 3 .

a) NQ//DA'// (BCC'B')
b) AN và BD cắt nhau, PB' và MN chéo nhau.
c) AMND.A'QPD' là hình lập phương
d) Diện tích xung quanh của hình hộp là 15000cm2


Đáp án A
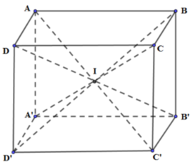
Phương pháp:
Xác định tỉ số chiều cao và tỉ số diện tích đáy của chóp I.ABCD và khối hộp ABCD.A’B’C’D’.
Cách giải:
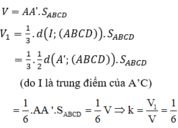
Đáp án B
Ta đặt AB=x, AD=y, AA'=z. Khi đó theo giả thiết ta có:
x y = 2 a 2 x z = 3 a 2 y z = 6 a 2 ⇔ x y = 2 a 2 x z = 3 a 2 y z = 6 a 2 x y z = 6 a 3 ⇔ x = a y = 2 a z = 3 a
Vậy thể tích khối hôp chữ nhật V=6a3.