Cho biểu thức f ( x ) = 1 2018 x + 2018 . Tính tổng
S = 2018 [ f ( - 2017 ) + f ( - 2016 ) + . . . + f ( 0 ) + f ( 1 ) + . . . + f ( 2018 ) ]
![]()
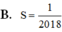
![]()
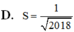
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A
Đặt
a = 2018 ⇒ f x + f 1 − x = 1 a x + a + 1 a 1 − x + a = a 1 − x + a x + 2 a a x + a a 1 − x + a = 1 a
Do đó
f x + f 1 − x = 1 2018

Đáp án A
Ta có f x + f 1 − x = 1 2018 x + 2018 + 1 2018 1 − x + 2018 = 1 2018 .
Suy ra S = 2018 2018 1 2018 = 2018.

Xét đa thức \(F\left(x\right)=ax^2+bx+c\)
\(F\left(0\right)=c=2016\)
\(F\left(1\right)=a+b+c=2017\Rightarrow a+b=1\) (1)
\(F\left(-1\right)=a-b+c=2018\Rightarrow a-b=2\) (2)
Từ (1), (2)
\(\Rightarrow\hept{\begin{cases}a+b-a+b=-1\\a+b+a-b=3\end{cases}}\Rightarrow\hept{\begin{cases}2b=-1\\2a=3\end{cases}}\Rightarrow\hept{\begin{cases}b=-0,5\\a=1,5\end{cases}}\)
\(\Rightarrow F\left(2\right)=1,5.2^2-0,5.2+2016=2021\)
Vậy \(F\left(2\right)=2021\).

Ta có
\(F\left(0\right)=2016\)
\(\Leftrightarrow a\cdot0^2+b\cdot0+c=2016\)
\(\Leftrightarrow0+0+c=2016\)
\(\Leftrightarrow c=2016\)
\(F\left(1\right)=2016\)
\(\Leftrightarrow a\cdot1^2+b\cdot1+c=2017\)
\(\Leftrightarrow a+b+c=2017\)
\(\Leftrightarrow a+b+2016=2017\)
\(\Leftrightarrow a+b=1\) \(\left(1\right)\)
\(F\left(-1\right)=2018\)
\(\Leftrightarrow a\cdot\left(-1\right)^2+b\cdot\left(-1\right)+c=2018\)
\(\Leftrightarrow a-b+c=2018\)
\(\Leftrightarrow a-b+2016=2018\)
\(\Leftrightarrow a-b=2\) \(\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)\(\Rightarrow a=\left(1+2\right)\div2=3\div2=1.5\)
\(\Rightarrow b=1-1.5=-0.5\)
Vậy \(F\left(x\right)=1.5x^2-0.5x+2016\)
\(\Leftrightarrow F\left(2\right)=1.5\cdot2^2-0.5\cdot2+2016\)
\(=1.5\cdot4-0.5\cdot2+2016\)
\(=6-1+2016=2021\)
Vậy \(F\left(2\right)=2021\)
nhớ k nha

f(0) = a.02 + b. 0 + c = 2016
<=> c =2016
f (1) = a.12 + b.1 + c =2017
<=> a + b =1 (1)
f ( -1 ) = a (-1)2 + b . (-1) +c =2018
<=> a -b =2 (2)
Từ (1),(2) <=> a = 1,5 ; b = -0,5
=> F(x) = 1,5x2 -0,5 x + 2016
F (2) = 1,5 . 22 -0,5 .2 +2016
= 6 -1 +2016 =2021
Ta có:
\(F\left(0\right)=a.0^2+b.0+c=2016\)
\(\Rightarrow c=2016\)
\(F\left(1\right)=a.1^2+b.1+c=2017\)
\(\Rightarrow a+b=1\)
\(F\left(-1\right)=a.\left(-1\right)^2+b.\left(-1\right)+c=2018\)
\(\Rightarrow a-b=2\)
Vì a + b =1 và a - b = 2 nên \(\Rightarrow a=\frac{3}{2};b=\frac{-1}{2}\)
Vậy \(F\left(2\right)=\frac{3}{2}.2^2-\left(\frac{-1}{2}\right).2+2016=2023\)

Lời giải:
Sử dụng công thức nội suy Newton:
$f(x)=a_1+a_2(x-2017)+a_3(x-2017)(x-2018)+a_4(x-2017)(x-2018)(x-t)$ với $a_4$ nguyên dương, $a_1,a_2, a_3, t$ bất kỳ.
Ta có:
$f(2017)=a_1=2018$
$f(2018)=a_1+a_2=2019$
$\Rightarrow a_2=1$. Thay giá trị $a_1,a_2$ vào lại $f(x)$ thì:
$f(x)=x+1+a_3(x-2017)(x-2018)+a_4(x-2017)(x-2018)(x-t)$
Do đó:
$f(2019)=2020+2a_3+2a_4(2019-a)$
$f(2016)=2017+2a_3+2a_4(2016-a)$
$\Rightarrow f(2019)-f(2016)=3+6a_4\vdots 3$ với mọi $a_4$ nguyên dương.
Cũng dễ thấy $3+6a_4>3$ với mọi $a_4$ nguyên dương
Do đó $f(2019)-f(2016)$ là hợp số (đpcm)


Theo bài ra ta có:
\(\hept{\begin{cases}c=2016\\a+b+c=2017\\a-b+c=2018\end{cases}\Leftrightarrow2a+2c=4035\Leftrightarrow2a=4035-2016.2=3}\)
\(\Leftrightarrow a=\frac{3}{2}\)
thay vào ta tính dc b nha