Tìm x, biết 1 x . x x 1 . x 1 x 2 . x 2 x 3 . x...

PT

Pham Trong Bach

27 tháng 10 2019

Tìm x, biết 1 x . x x + 1 . x + 1 x + 2 . x + 2 x + 3 . x + 3 x + 4 . x + 4 x + 5 . x + 5 x + 6 = 1 A. x = -6 B. x = -5 C. x = -7 D. x =...

Đọc tiếp

#Toán lớp 8

1

CM

Cao Minh Tâm

27 tháng 10 2019

Đúng(0)

NQ

Nguyễn Quang Huy

16 tháng 8 2021

. Tìm x biết rằng:

a)(x + 1)3 – (x + 2)(x – 1)2 – 3(x – 3)(x + 3) = 5

b)(x + 1)3 + (x – 1)3 = (x + 2)3 + (x – 2)3

c) (x + 1)3 - (x - 1)3 - 6(x - 1)2 = -10

#Toán lớp 8

2

NL

Nguyễn Lê Phước Thịnh

16 tháng 8 2021

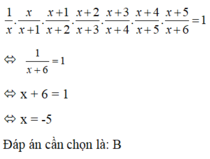
a: Ta có: \(\left(x+1\right)^3-\left(x+2\right)\left(x-1\right)^2-3\left(x-3\right)\left(x+3\right)=5\)

\(\Leftrightarrow x^3+3x^2+3x+1-\left(x+2\right)\left(x^2-2x+1\right)-3\left(x^2-9\right)=5\)

\(\Leftrightarrow x^3+3x^2+3x+1-\left(x^3-2x^2+x+2x^2-4x+2\right)-3\left(x^2-9\right)=5\)

\(\Leftrightarrow x^3+3x^2+3x+1-x^3+3x-2-3x^2+9=5\)

\(\Leftrightarrow6x=-3\)

hay \(x=-\dfrac{1}{2}\)

b: Ta có: \(\left(x+1\right)^3+\left(x-1\right)^3=\left(x+2\right)^3+\left(x-2\right)^3\)

\(\Leftrightarrow x^3+3x^2+3x+1+x^3-3x^2+3x-1=x^3+6x^2+12x+8+x^3-6x^2+12x-8\)

\(\Leftrightarrow2x^3+6x=2x^3+24x\)

\(\Leftrightarrow x=0\)

c: Ta có: \(\left(x+1\right)^3-\left(x-1\right)^3-6\left(x-1\right)^2=-10\)

\(\Leftrightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+12x-1=-10\)

\(\Leftrightarrow12x=-11\)

hay \(x=-\dfrac{11}{12}\)

Đúng(2)

VT

Vũ Thị Hoài Phương

6 tháng 12 2021

(X-1)^3 = (1-x)^2

Đúng(1)

H

hee???

20 tháng 12 2021

1, Tìm x, biết \(x^2\) – 36 = 0
A. x = 6. B. x = -6.
C. x = 6; x = -6. D. x = 36 hoặc x = - 36.
2, Tìm x, biết \(x^3\) – 3\(x^2\) + 3x - 1 = 0

A. x = 1. B. x = -1. C. x = 0. D. x = 2.

#Toán lớp 8

1

DT

Đỗ Tuệ Lâm

20 tháng 12 2021

1C

2A

Đúng(0)

MM

Moon Moon

18 tháng 10 2017 - olm

1)Tìm x thỏa mãn: /x-1/+x-2/+/x-3/+/x-4/=3

2) Tìm x, biết: /x+1/-x+2/-/x+3/x...-/x+100/=605x

#Toán lớp 7

0

NL

Ng Linhhh

25 tháng 12 2022

Tìm x biết.

1) 3(x-2) + 4(x-1) = 25 2) (5x-3)(x-2) = (x-1)(x-2) 3) (x-2)² = 4(x-1)²

#Toán lớp 8

3

TM

Trần Minh Hiếu

25 tháng 12 2022

\(3\left(x-2\right)+4\left(x-1\right)=25\)

\(\Leftrightarrow3x-6+4x-4=25\)

\(\Leftrightarrow7x=35\)

\(\Leftrightarrow x=5\)

Đúng(1)

TM

Trần Minh Hiếu

25 tháng 12 2022

\(\left(5x-3\right)\left(x-2\right)=\left(x-1\right)\left(x-2\right)\)

\(\Leftrightarrow\left(5x-3\right)\left(x-2\right)-\left(x-1\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(5x-3-x+1\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(4x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\4x+2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{-1}{2}\end{matrix}\right.\)

Đúng(1)

LM

Lục Mão Thiên

12 tháng 1 2020 - olm

Tìm x biết (1 - x)/(x^2 + x + 1) - (x - 1)/(x^2 - x + 1) = 3/[x.(x^4 + x^2 + 1)]

#Toán lớp 8

2

D

阮草~๖ۣۜDαɾƙ

12 tháng 1 2020

\(\frac{1-x}{x^2+x+1}-\frac{x-1}{x^2-x+1}=\frac{3}{\left[x\left(x^4+x^2+1\right)\right]}\)

\(\Leftrightarrow\frac{\left(1-x\right)x\left(x^2-x+1\right)\left(x^4+x^2+1\right)}{x\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^4+x^2+1\right)}\)\(-\)\(\frac{x\left(x-1\right)\left(x^2+x+1\right)\left(x^4+x^2+1\right)}{x\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^4+x^2+1\right)}\)\(=\)\(\frac{3\left(x^2-x+1\right)\left(x^2+x+1\right)}{x\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^4+x^2+1\right)}\)

\(\Rightarrow\left(1-x\right)x\left(x^2-x+1\right)\left(x^4+x^2+1\right)-x\left(x-1\right)\left(x^2+x+1\right)\left(x^4+x^2+1\right)=\)\(3\left(x^2-x+1\right)\left(x^2+x+1\right)\)

\(\Leftrightarrow\left(x-x^2\right)\left(x^2-x+1\right)\left(x^4+x^2+1\right)-\left(x^2-x\right)\left(x^2+x+1\right)\left(x^4+x^2+1\right)=\)\(\left(3x^2-3x+3\right)\left(x^2+x+1\right)\)

\(\Leftrightarrow\left(x^3-x^2+x-x^4+x^3-x^2\right)\left(x^4+x^2+1\right)-\left(x^4+x^3+x^2-x^3-x^2-x\right)\left(x^4+x^2+1\right)=\) \(3x^4+3x^3+3x^2-3x^3-3x^2-3x+3x^2+3x+3\)

\(\Leftrightarrow\left(2x^3-2x^2+x-x^4\right)\left(x^4+x^2+1\right)-\left(x^4-x\right)\left(x^4+x+1\right)=3x^4+3x^2+3\)

\(\Leftrightarrow\left(x^4+x^2+1\right)\left(2x^3-2x^2+x-x^4-x^4+x\right)=3x^4+3x^2+3\)

\(\Leftrightarrow\left(x^4+x^2+1\right)\left(2x^3-2x^2+2x-2x^4\right)=3x^4+3x^2+3\)

\(\Leftrightarrow2x^7-2x^6+2x^5-2x^8+2x^5-2x^4+2x^3-2x+2x^3-2x^2+2x-2x^4-3x^4-3x^2-3=0\)

\(\Leftrightarrow2x^7-2x^6+4x^5-2x^8-7x^4+x^2-3=0\)

Đến đây thì chịu òi :^ Sr nha

Đúng(2)

TP

Trần Phúc Khang

13 tháng 1 2020

\(\frac{1-x}{x^2+x+1}-\frac{x-1}{x^2-x+1}=\frac{3}{x\left(x^4+x^2+1\right)}\)

Ta có \(x^4+x^2+1=\left(x^2+1\right)^2-x^2=\left(x^2-x+1\right)\left(x^2+x+1\right)\)

=> \(\left(1-x\right)\left(\frac{1}{x^2+x+1}+\frac{1}{x^2-x+1}\right)=\frac{3}{x\left(x^4+x^2+1\right)}\)

<=>\(\left(1-x\right)\left(2x^2+2\right).x=3\)

Do \(2x^2+2>0\)

=> \(\left(1-x\right).x>0\)

=> \(0< x< 1\)=> \(2x^2+2< 4\)

Pt<=> \(\left(x-x^2\right)\left(2x^2+2\right)=3\)

Mà \(x-x^2\le\frac{1}{4};2x^2+2< 4\)

=> \(VT< 1\)

=> PT vô nghiệm

Đúng(0)

E

êrgsrgrg

24 tháng 9 2021

: Tìm x biết

a) (x + 1)³x – x( x -2)² + x -1 = 0

b) ( x – 2)³ – x²(x -6) =4

c) ( x -1)( x² + x + 1) – x( x+2)(x -2) =5

d) 3(x -1)² – 3x( x -5) =1

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

24 tháng 9 2021

b: Ta có: \(\left(x-2\right)^3-x^2\left(x-6\right)=4\)

\(\Leftrightarrow x^3-6x^2+12x-8-x^3+6x^2=4\)

\(\Leftrightarrow12x=12\)

hay x=2

d: Ta có: \(3\left(x-1\right)^2-3x\left(x-5\right)=1\)

\(\Leftrightarrow3x^2-6x+3-3x^2+15x=1\)

\(\Leftrightarrow9x=-2\)

hay \(x=-\dfrac{2}{9}\)

Đúng(0)

HT

Hoàng Thị Huyền Trang

25 tháng 7 2020 - olm

bài 1 : tìm x biết a, ( x - 2 ) : 2 x 3 = 6b, X : ( hỗn số 3 1/2 x hỗn số 2 2/3 ) = 9/56c, 1 + 3 + 5 + .....+ ( 2 x X + 1 ) = 625bài 2 : tìm x biếta, ( x - 1/2 ) x 5/3 = 7/4 - 1/2b, 5 x X + X = 42c, ( x+1 ) + ( x+ 3 ) + ( x + 5 ) + ....+ ( x + 11 ) = 58bài 3 tìm x biếta, X - 1,25 x 4 = 7,5b, X = ( hỗn số 6 3/5 : 6 - 0 , 125 x 8 + hỗn số 2 2/15 x 0,03 ) x 2/11c, ( X + 1 ) +(X + 2 ) + ( X + 3 ) + ....+(X + 20 ) =...

Đọc tiếp

#Toán lớp 6

1

TT

Trí Tiên亗

26 tháng 7 2020

1

\(\left(x-2\right):2.3=6\)

\(\Leftrightarrow\left(x-2\right):2=2\)

\(\Leftrightarrow\left(x-2\right)=4\)

\(\Leftrightarrow x=4+2=6\)

c) ta có

\(\left[\left(2x+1\right)+1\right]m:2=625\)

\(\Leftrightarrow\left[\left(2x+1\right)+1\right]\left\{\left[\left(2x+1\right)-1\right]:2+1\right\}=1250\)

\(\Leftrightarrow\left(2x+1\right)^2+1-1:2+1=1250\)

\(\Leftrightarrow\left(2x+1\right)^2+1-2+1=1250\)

\(\Leftrightarrow\left(2x+1\right)^2+1-2=1249\)

\(\Leftrightarrow\left(2x+1\right)^2+1=1251\)

\(\Leftrightarrow\left(2x+1\right)^2=1250\)

...

2

\(\left(x-\frac{1}{2}\right).\frac{5}{3}=\frac{7}{4}-\frac{1}{2}\)

\(\Leftrightarrow\left(x-\frac{1}{2}\right).\frac{5}{3}=\frac{5}{4}\)

\(\Leftrightarrow\left(x-\frac{1}{2}\right)=\frac{5}{4}:\frac{5}{3}\)

\(\Leftrightarrow\left(x-\frac{1}{2}\right)=\frac{5}{4}.\frac{3}{5}\)

\(\Leftrightarrow x-\frac{1}{2}=\frac{3}{4}\)

\(\Leftrightarrow x=\frac{3}{4}+\frac{1}{2}=\frac{5}{4}\)

Đúng(0)

DN

dũng nguyễn đăng

5 tháng 9 2021

tìm x, biết :

d)(x - 3)(x^2 + 3x + 9) + x(x + 2)(2 - x) = 1

e) (x + 1)^3 - (x - 1)^3 - 6(x - 1)^2 = -19

#Toán lớp 8

2

KK

Kirito-Kun

5 tháng 9 2021

d. (x - 3)(x² + 3x + 9) + x(x + 2)(2 - x) = 1

<=> x³ - 9 + (x² + 2x)(2 - x) = 1

<=> x³ - 9 + 2x² - x³ + 4x - 2x² = 1

<=> 4x = 10

<=> x = \(\dfrac{10}{4}=\dfrac{5}{2}\)

Đúng(1)

S

Shauna

5 tháng 9 2021

d)(x - 3)(x^2 + 3x + 9) + x(x + 2)(2 - x) = 1

\(<=> x^3-27-x(x^2-4)=1\)

\(<=> x^3-27-x^3-4x=1<=>-4x=28<=> x=-7\)

=> ptrình có tập nghiệm S={-7}

e) (x + 1)^3 - (x - 1)^3 - 6(x - 1)^2 = -19

\(<=> x^3+3x^2+3x+1-(x^3-3x^2+3x-1)-6(x^2-2x+1)+19=0\)

\(<=>x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+12x-6+19=0\)

\(<=>12x=15<=>x=12/15 \)

=> ptrình có tập nghiệm S={12/15}

Đúng(1)

ND

Ninh Đỉnh Quân

4 tháng 4 2023 - olm

1. Tìm X, biết: x - \(\dfrac{2}{3}\) x ( X + 9 ) = 1

2. Tìm X, biết: X - \(\dfrac{11}{15}\) = \(\dfrac{3+X}{5}\)

#Toán lớp 4

2

NT

Nguyễn thành Đạt

CTVHS

4 tháng 4 2023

\(1.x-\dfrac{2}{3}\times\left(x+9\right)=1\)

\(x-\dfrac{2}{3}\times x-6=1\)

\(x\times\left(1-\dfrac{2}{3}\right)=7\)

\(x\times\dfrac{1}{3}=7\)

\(x=21\)

\(2.x-\dfrac{11}{15}=\dfrac{3+x}{5}\)

\(\dfrac{15x}{15}-\dfrac{11}{15}=\dfrac{9+3x}{15}\)

\(15x-11=9+3x\)

\(12x=20\)

\(x=\dfrac{5}{3}\)

Đúng(2)

MM

mèo mập(❤️ ω ❤️)

4 tháng 4 2023

Đúng(0)

DN

Đinh Nữ Ngọc Như

13 tháng 1 2022

1.tìm x,y biết

a, x.(y-3)≥0

b, (2.x-1).(y-1)≤0

c,(x-1).(2.k+1)≥0

2. tìm x,y ϵ Z biết

a, x(x+3)=0

b,(x-2).(5-x)=0

c,(x-1).(x^2+1)=0

d, x.y+3.x-7.y=21

e,x.y+3.x-2y=11

#Toán lớp 6

1

NL

Nguyễn Lê Phước Thịnh

13 tháng 1 2022

Bài 2:

a: =>x=0 hoặc x+3=0

=>x=0 hoặc x=-3

b: =>x-2=0 hoặc 5-x=0

=>x=2 hoặc x=5

c: =>x-1=0

hay x=1

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP