So sánh hai phân số:
a ) 3 5 v à 1 5 ; b ) 9 10 v à 11 10 c ) 13 17 v à 15 17 ; d ) 25 19 v à 22 19
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
23 tháng 7 2019
Đúng(0)
Những câu hỏi liên quan
17 tháng 2 2022
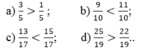
1.a) 3/4 > 5/10
b) 35/25 > 16/14
2.a) 7/5 > 5/7
b) 14/16 < 24/21
HT nha
( bạn t.i.c.k cho mik nha, mik cảm ơn )
1 tháng 4 2018
b) \(\frac{5}{9}\)và \(\frac{5}{8}\) :Quy đồng mẫu số : \(\frac{5}{9}\) = \(\frac{5.8}{9.8}\) = \(\frac{40}{72}\) ; \(\frac{5}{8}\) = \(\frac{5.9}{8.9}\) = \(\frac{45}{72}\)
Vì \(\frac{40}{72}\) < \(\frac{45}{72}\) nên \(\frac{5}{9}\) < \(\frac{5}{8}\)
c)\(\frac{8}{7}\) và \(\frac{7}{8}\) :Quy đồng mẫu số: \(\frac{8}{7}\) = \(\frac{8.8}{7.8}\) = \(\frac{64}{56}\) ; \(\frac{7}{8}\) = \(\frac{7.7}{8.7}\) =\(\frac{49}{56}\)
Vì \(\frac{64}{56}\) > \(\frac{49}{56}\) nên \(\frac{8}{7}\) > \(\frac{7}{8}\)
bạn an đông à cái câu A của bạn sai một chút.
CHÚC BẠN HỌC TỐT !
1 tháng 4 2018
a)\(\frac{3}{7}\) và\(\frac{2}{8}\) :Quy đồng mẫu số : \(\frac{3}{7}\) = \(\frac{3.8}{7.8}\) = \(\frac{24}{56}\) ; \(\frac{2}{8}\) = \(\frac{2.7}{8.7}\) = \(\frac{14}{56}\)
Vì \(\frac{24}{56}\) > \(\frac{14}{56}\) nên \(\frac{3}{7}\) > \(\frac{2}{8}\)
VN
24 tháng 1 2017
Bài 1: Quy đồng => so sánh => trả về phân số ban đầu
Bài 2: Như bài 1
14 tháng 10 2021
Bài 1
a) 4/3 < 1/3
b) 2/5 < 3/2
c) 7/2 > 1/4
d) 3/4 < 5/6
Bài 2
a) 6/10 = 3/5 và 4/5 vậy 3/5 < 4/5
b) 3/4 và 6/12 = 1/2 vậy 3/4 > 1/2
PL
13 tháng 2 2017
1 so sánh 2 phân số
a, 3/4 = 3 x 10 / 4 x 10 = 30/40; 5/10 = 5 x 4 / 10 x 4 = 20/40. Vì 30/40 >20/40 nên 3/4 >5/10
b, 35/25 = 35 x 14 / 25 x 14 = 490/350; 16/14 = 16 x 25 / 14 x 25 = 400/350. Vì 490/350 >400/350 nên 35/25 >16/14
2
a, Cách 1: 7/5 = 7 x 7/ 5 x 7 = 49/35; 5/7 =5 x 5/ 7 x5 = 25/35. Vì 49/35> 25/35 nên 7/5> 5/7
Cách 2 : Ta có thể so sánh với 1 mà không cần quy đồng: Vì 7/5 >1 và 5/7 <1 nên 7/5 > 5/7
b, Cách 1: 14/16 = 14 x 21/ 16 x 21 = 294/336; 24/21 = 24 x 16/ 21 x 16 = 384/336. Vì 294/336 < 384/336 nên 14/16 < 24/21
Cách 2: Tương tự như vậy ta có: Vì 14/16 <1 và 24/21 >1 nên 14/16< 24/21
THế thôi tk mình nhé mình sẽ tk lại cho mà
12 tháng 2 2023
a
2/5> 2/7
5/9<5/6
11/2>11/3
cách so sánh :
sét mẫu số của phân số này bé hơn mẫu số của phân số kia thì phân số này lớn hơn
mẫu số của phân số này lớn hơn mẫu số của phân số kia thì phân số này bé hơn
CH
Cô Hoàng Huyền
Admin
VIP
23 tháng 6 2017
1) \(A=\left(\sqrt{7-\sqrt{21}+4\sqrt{5}}\right)^2=7-\sqrt{21}+4\sqrt{5}\)
\(B=\left(\sqrt{5}-1\right)^2=6-2\sqrt{5}\)
\(\Rightarrow A-B=1-\sqrt{21}+6\sqrt{5}=\left(1+\sqrt{180}\right)-\sqrt{21}>0\)
\(\Rightarrow A>B\Rightarrow\sqrt{7-\sqrt{21}+4\sqrt{5}}>\sqrt{5}-1\)
2) \(C=\left(\sqrt{5}+\sqrt{10}+1\right)^2=5+10+1+10\sqrt{2}+2\sqrt{5}+2\sqrt{10}\)
\(=26+10\sqrt{2}+2\sqrt{5}+2\sqrt{10}>26+10>35=\left(\sqrt{35}\right)^2\)
Vậy \(\sqrt{5}+\sqrt{10}+1>\sqrt{35}\)
3) \(\left(\frac{15-2\sqrt{10}}{3}\right)^2=\frac{225-60\sqrt{10}+40}{9}=\frac{265-60\sqrt{10}}{9}=\frac{265}{9}-\frac{20\sqrt{10}}{3}< 15\)
Vậy nên \(\frac{15-2\sqrt{10}}{3}< \sqrt{15}\)
5 tháng 9 2019
\(\sqrt[3]{\left(1-\sqrt{3}\right)\left(4-2\sqrt{3}\right)}=\sqrt[3]{\left(1-\sqrt{3}\right)\left(\sqrt{3}-1\right)^2}\)=\(\sqrt[3]{\left(1-\sqrt{3}\right)^3}\)=1-\(\sqrt{3}\)
\(\sqrt[3]{\left(1-\sqrt{5}\right)\left(6-2\sqrt{5}\right)}=\sqrt[3]{\left(1-\sqrt{5}\right)\left(\sqrt{5}-1\right)^2}\)=\(\sqrt[3]{\left(1-\sqrt{5}\right)^3}\)=1-\(\sqrt{5}\)
Ta thấy \(\sqrt{5}>\sqrt{3}\)nên 1-\(\sqrt{3}\)>\(1-\sqrt{5}\)
Vậy \(\sqrt[3]{\left(1-\sqrt{3}\right)\left(4-2\sqrt{3}\right)}\)>\(\sqrt[3]{\left(1-\sqrt{5}\right)\left(6-2\sqrt{5}\right)}\)
27 tháng 6 2019
\(\text{a, }2^{30}=8^{10}\)
\(\text{ }3^{20}=\left(3^2\right)^{10}=9^{10}\)
\(\text{Vậy }2^{30}< 3^{20}\)
27 tháng 6 2019
\(\text{b, }5^{300}=\left(5^3\right)^{100}=125^{100}\)
\(3^{500}=\left(3^5\right)^{100}=243^{100}\)
\(\text{Vậy }5^{300}< 243^{100}\)
