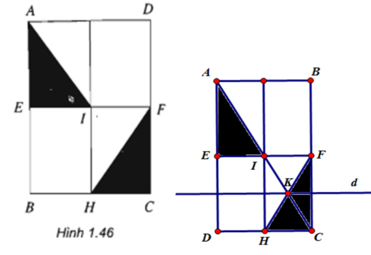
Cho hình chữ nhật ABCD. Gọi E, F, H, I theo thứ tự là trung điểm của các cạnh AB, CD, BC, EF. Hãy tìm một phép dời hình biến tam giác AEI thành tam giác FCH (h.1.46)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 6 2018
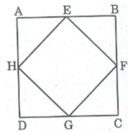
Chứng minh EFGH là hình bình hành. Để EFGH là hình chữ nhật thì
Þ H E F ^ = 90 0 ⇒ H E ⊥ E F
Þ AC ^BD.
CM
14 tháng 5 2017
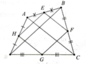
* Ta có EF là đường trung bình của ∆ ABC
Suy ra: EF //AC và EF = 1/2 AC (1)
* Trong ∆ ADC có HG là đường trung bình
Suy ra: HG // AC và HG = 1/2 AC (2)
Từ (l) và (2) suy ra EF // HG và EF = HG
Vậy tứ giác EFGH là hình bình hành.
Tứ giác EFGH là hình chữ nhật ⇔ EH ⊥ EF ⇔ AC ⊥ BD
CM
5 tháng 9 2017
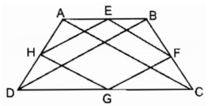
Trong ∆ ABD ta có:
E là trung điểm của AB (gt)
H là trung điểm của AD (gt)
nên EH là đường trung bình của ∆ ABD
⇒ EH // BD và EH = 1/2 BD (tính chất đường trung bình của tam giác) (1)
- Trong ∆ CBD ta có:
F là trung điểm của BC (gt)
G là trung điểm của CD (gt)
nên FG là đường trung bình của ∆ CBD
⇒ FG // BD và FG = 1/2 BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: EH // FG và EH = FG
Suy ra: Tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Trong ∆ ABC ta có:
EF là đường trung bình
⇒ EF = 1/2 AC (tính chất đường trung bình của tam giác) (3)
AC = BD (tính chất hình thang cân) (4)
Từ (1), (3) và (4) suy ra: EH = EF
Vậy : Tứ giác EFGH là hình thoi.
CM
16 tháng 6 2017
Đáp án A:
Đ O Δ O C F = Δ O A E V A ; 2 Δ O A E = Δ C A B
Đáp án B:
Đ A C Δ O C F = Δ O C M V C ; 2 Δ O C M = Δ A C B
Đáp án C:
V C ; 2 Δ O C F = Δ A C D Đ O Δ A C D = Δ C A B
Đáp án D:
Đ B D Δ O C F = Δ O A N V O ; − 1 Δ O A N = Δ O C M
Vậy phép đồng dạng P được hợp thành bởi phép đối xứng trục BD và phép vị tự tâm O, tỉ số k = -1 không biến tam giác OCF thành tam giác CAB.
Đáp án D
CM
7 tháng 12 2017
Đ E I ( 1 ) = ( 8 ) ; T D I → ( 8 ) = ( 3 ) .
A. Phép đối xứng tâm I và phép đối xứng trục IB thì (1) không biến thành hình nào từ (2) đến (8).
B. Phép đối xứng tâm I và phép quay tâm I góc quay 90 o (1) không biến thành hình nào từ (2) đến (8)
D.phép tịnh tiến theo A I → và phép đối xứng tâm I thì hình (1) thành hình (2)
Đáp án C
- Phép đối xứng qua tâm I biến ΔAEI thành ΔCFI
- Phép đối xứng qua trục d biến ΔCFI thành ΔFCH