Viết phương trình tham số, phương trình chính tắc của đường thẳng ∆ trong các trường hợp sau: ∆ đi qua hai điểm C(1; -1; 1) và D(2; 1; 4)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 9 2018
Phương trình tham số của đường thẳng Δ đi qua điểm A(1; 2; 3) và có vecto chỉ phương
a
→
= (3; 3; 1) là: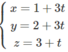 
Phương trình chính tắc của ∆ là:
CM
14 tháng 11 2019
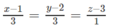
∆ ⊥ ( α ) ⇒ a ∆ → = a α → = (2; −1; 1)
Phương trình tham số của ∆ là
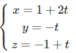
Phương trình chính tắc của ∆ là:
CM
26 tháng 6 2017
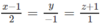
vecto chỉ phương của d là a = PQ = (4;2;1) (vì d đi qua hai điểm P(1;2;3),Q(5;4;4)
Vậy pt tham số của đường thẳng d là: x = 1 + 4 t y = 2 + 2 t z = 3 + t
CM
8 tháng 5 2019
Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)
Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)
Vậy đường thẳng Δ có dạng: x+y-3=0
Vì đường tròn có tâm I thuộc d nên I(a;-a)
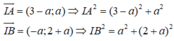
Vì đường tròn đi qua A, B nên I A 2 = I B 2 ⇒ (3 - a ) 2 + a 2 = a 2 + (2 + a ) 2 ⇔ (3 - a ) 2 = (2 + a ) 2
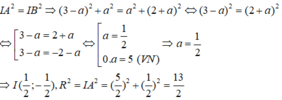
Vậy phương trình đường tròn có dạng:
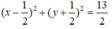
Ta có:
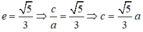
Giả sử elip (E) có dạng:
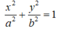
Vì (E) đi qua B nên:
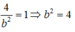
Mà
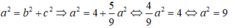
Vậy phương trình chính tắc của elip (E) là:
13 tháng 4 2023
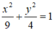
1: (E): x^2/a^2+y^2/b^2=1
Thay x=0 và y=3 vào (E), ta được:
3^2/b^2=1
=>b^2=9
=>b=3
F2(5;0)
=>c=5
=>\(\sqrt{a^2-9}=5\)
=>a^2-9=25
=>a^2=34
=>\(a=\sqrt{34}\)
=>x^2/34+y^2/9=1
2: Thay x=7 và y=0 vào (E), ta được:
7^2/a^2+0^2/b^2=0
=>a^2=49
=>a=7
Thay x=0 và y=3 vào (E), ta được:
0^2/a^2+3^2/b^2=1
=>b^2=9
=>b=3
=>(E): x^2/49+y^2/9=1
3: Thay x=0 và y=1 vào (E), ta được:
1/y^2=1
=>y=1
=>(E): x^2/a^2+y^2/1=1
Thay x=1 và y=căn 3/2 vào (E), ta được:
1^2/a^2+3/4=1
=>1/a^2=1/4
=>a^2=4
=>a=2
=>(E); x^2/4+y^2/1=1
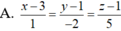
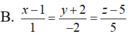
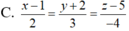
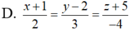
∆ đi qua hai điểm C và D nên có vecto chỉ phương CD → = (1; 2; 3)
Vậy phương trình tham số của ∆ là
Phương trình chính tắc của ∆ là: