Vẽ đường tròn tâm O, bán kính R = 3cm.Vẽ một đường kính AB. Vẽ tiếp một dây cung CD (hai điểm C, D không trùng với các điểm A,B và ba điểm C, O, D không thẳng hàng). Nếu lấy n điểm (phân biệt) trên đường tròn đó ta có được bao nhiêu cung
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 5 2017
Với hai điểm (phân biệt) trên một đường tròn ta có được 2 cung có mút là hai điểm đó. Với n điểm (phân biệt) cho trước trên một đường tròn, thì cứ lấy 2 trong số n điểm đó ta được 2 cung, vì vậy có tất cả n(n-1) cung trên đường tròn đó.
CM
4 tháng 3 2019
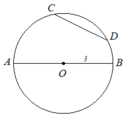
Giả sử vẽ được như hình bs.18
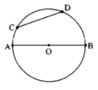
Dùng compa so sánh được CD < AB.
CM
2 tháng 3 2017
Giả sử vẽ được như hình bs.18
Khi đó, có các cung là: AC nhỏ, AD nhỏ, AB hay cung ACDBm BA (cung nửa đường tròn không đi qua C và D) , ABD hay cung AD lớn, ABDC hay cung AC lớn, BD nhỏ, BC nhỏ, BAC hay cung BC lớn, BACD hay cung BD lớn, CD nhỏ, CABD hay CD lớn.
18 tháng 5 2022
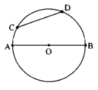
a: Tên các cung là CA;AD;CB;DB
b: Vì AB là đường kính
và CD là dây
nên AB>CD
c: Ta sẽ được n(n-1) cung
CM
30 tháng 1 2018
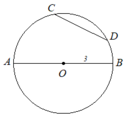
Các cung là AC nhỏ, AD nhỏ, AD hay cung ACDB, AB (cung nửa đường tròn không đi qua C và D), ABD hay cung AD lớn, cung ABC hay cung AC lớn. Cung BD nhỏ, BC nhỏ, BAC hay cung BC lớn, BACD hay cung BD lớn, cung CD nhỏ, CABD hay CD lớn
8 tháng 3 2023
1: ΔOAB cân tại O
mà OI là trung tuyến
nên OI vuông góc AB
góc OIM=góc OCM=góc ODM=90 độ
=>O,I,M,D,C cùng thuộc đường tròn đường kính OM
góc DIM=góc MOD
góc CIM=góc COM
mà góc COM=góc DOM
nên góc DIM=góc CIM
=>IM là phân giác của góc CID
CM
7 tháng 8 2018
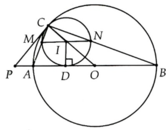
a, Vẽ tiếp tuyến tại C cắt đường AB ở P. Phân giác C P B ^ cắt OC ở I. Vẽ đường tròn tâm I bán kính IC, đó là đường tròn cần tìm
b, Do A C B ^ = 90 0 nên M C N ^ = 90 0
=> MN là đường kính của (I) => ĐPCM
c, Chứng minh được MN//AB nên ID ^ MN => M D ⏜ = N D ⏜ hay CD là tia phân giác A C B ^ => Đpcm
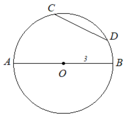
Giả sử vẽ được như hình bs.18
Với hai điểm (phân biệt) trên một đường tròn ta có được hai cung có mút là hai điểm đó. Với n điểm (phân biệt) cho trước trên một đường tròn, thì cứ lấy 2 trong số n điểm đó ta được 2 cung, vì vậy có tất cả n(n – 1) cung trên đường tròn đó.