Cho góc xOy, phân giác Ot. Trên Ox lấy các điểm A và C' sao cho O A = 4 c m , O C ' = 9 c m , trên Oy lấy các điểm A' và C sao cho O A ' = 12 c m , O C = 3 c m , trên tia Ot lấy các điểm B và B' sao cho O B = 6 c m , O B ' = 18 c m . Chứng minh
a) Δ O A B ∽ Δ O A ' B ' ;
b) A B A ' B ' = A C A ' C ' = B C B ' C ' .

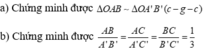
 AC) (1)
AC) (1)