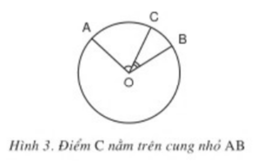
Hãy chứng minh đẳng thức sd A B ^ = sd A C → + sd C B ^ trong trường hợp điểm C nằm trên cung nhỏ AB (h.3).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 9 2019
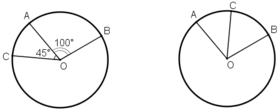
* Trường hợp 1 . Điểm C nằm trên cung lớn AB.
Do điểm C nằm trên cung lớn AB nên tia OA nằm giữa hai tia OB và OC.
Do 
nên tia OA nằm giữa hai tia OB và OC hay A nằm trên cung BC.
Suy ra: 
=
100
0
+
45
0
=
145
0
Khi đó, số đo cung nhỏ BC là
145
°
( bằng góc ở tâm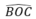 
)
Số đo cung lớn BC là: 360 0 − 145 0 = 215 0
* Trường hợp 2: Điểm C nằm trên cung nhỏ AB
Vì điểm C nằm trên cung nhỏ AB nên OC nằm giữa OA và OB
Ta có: 
=
100
0
−
45
0
=
55
0
Khi đó, số đo cung nhỏ BC là 55 0
Số đo cung lớn BC là: 360 0 − 55 0 = 305 0
Kiến thức áp dụng
+ Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
+ Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+ Số đo của cung lớn bằng hiệu của 360º và số đo của cung nhỏ (có chung hai mút với cung lớn).
AN
12 tháng 6 2020
c) C/m: \(\widehat{OMB}=90^o\) (vì M là tđ của BH => \(OM\perp BH\))
=> M thuộc cung tròn đường kính OB cố định...
CM
20 tháng 12 2019
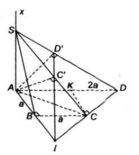
a) Ta có:
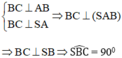
Gọi K là trung điểm của AD ta có CK = AB = AD/2 nên tam giác ACD vuông tại C
Ta có:
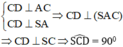
b) Trong mặt phẳng (SAC) vẽ AC’ ⊥ SC và trong mặt phẳng (SAD) vẽ AD’ ⊥ SD
Ta có AC’⊥ CD (vì CD ⊥ (SAC))
Và AC’ ⊥ SC nên suy ra AC’ ⊥ (SCD) ⇒ AC’ ⊥ SD
Ta lại có AB ⊥ AD và AB ⊥ SA nên AB ⊥ (SAD) ⇒ AB ⊥ SD
Ba đường thẳng AD’, AC’ và AB cùng đi qua điểm A và vuông góc với SD nên cùng nằm trong mặt phẳng (α) qua A và vuông góc với SD
c) Ta có C’D’ là giao tuyến của (α) với mặt phẳng (SCD). Do đó khi S di động trên tia Ax thì C’D’ luôn luôn đi qua một điểm cố định là giao điểm của AB và CD
AB ⊂ (α), CD ⊂ (SCD) ⇒ I ∈ (α) ∩ (SCD) = C’D’
19 tháng 4 2020
no no no no no no no no no no ko bít nha bạn hình như đề bài sai
nha nha nha nha nha nha nha nha nha nha tụi nghiệp con bứ
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2022
Ta có: \(SB=4MB=4\left(SB-SM\right)\Rightarrow\dfrac{SM}{SB}=\dfrac{3}{4}\)
Tương tự: \(\dfrac{SN}{SD}=\dfrac{3}{4}\)
\(\Rightarrow\dfrac{SM}{SB}=\dfrac{SN}{SD}\)
\(\Rightarrow MN||BD\) (định lý Talet đảo)
\(\Rightarrow BD||\left(MNP\right)\)
Vì C nằm trên cung nhỏ AB nên OC nằm giữa OA và OB