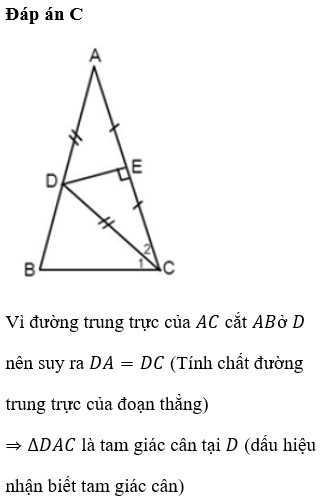
Cho Δ A B C cân tại A. Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của A C B ^ . Tính các góc của Δ A B C
A. A ^ = 30 0 , B ^ = C ^ = 75 0
B. A ^ = 40 0 , B ^ = C ^ = 70 0
C. A ^ = 36 0 , B ^ = C ^ = 72 0
D. A ^ = 70 0 , B ^ = C ^ = 55 0